Grafisches Ableiten?
Hallo, ich habe sehr schwerliegende Probleme mit dem grafischen Ableiten. Und zwar weiß ich nicht wie man von einer gegebenen 1.Ableitung wieder zur Ausgangsfunktion kommt und kann auch die folgenden Fragen deswegen nicht beantworten ._. Es wäre nett, wenn ihr mir helfen würdet. Danke im Voraus
4 Antworten
Für die Aufgabe brauchst du die Funktion f(x) nicht. Du hast ja geschrieben, dass f'(x) gegeben ist.
Mit dieser Funktion lassen sich sowohl die extremstellen der Funktion f(x) bestimmen (und ob diese hoch- oder tiefpunkte sind) , als auch die Steigung der tangente von f an allen Stellen und somit auch die Steigung von f an allen Stellen.
Ich hoffe, das klärt deine Frage.
Was ich immer gemacht hab ist grafisch integrieren ( also wieder auf die stammfunktion), damit ich schon mal ungefähr weis, wie f aussieht. Das geht mit der NEW Regel recht gut. Du schreibst NEW zweimal untereinander, aber das zweite mal so eingerückt, dass das N unter dem E steht. N ist eine Nullstelle, E ein Extrempunkt und W eine Wendestelle. Das obere NEW ist f, das untere f'
Du schaust jetzt einfach wo f' eine Nullstelle hat und das ist bei f ein Extrempunkt, also du schaust einfach bei den zwei NEWs was untereinander steht und gehst von unten nach oben. ( das N steht unter dem E)
So kannst du den Graph grob einzeichnen, hier wäre das ein steigender Graph mit einem Sattelpunkt ( steigend weil die Ableitung, die wir sehen dauerhaft ÜBER der x- Achse liegt.
Ich finde es viel einfacher die Fragen zu beantworten, wenn ich ungefähr weis, wie die Funktion aussieht.
Hoffe ich konnte helfen
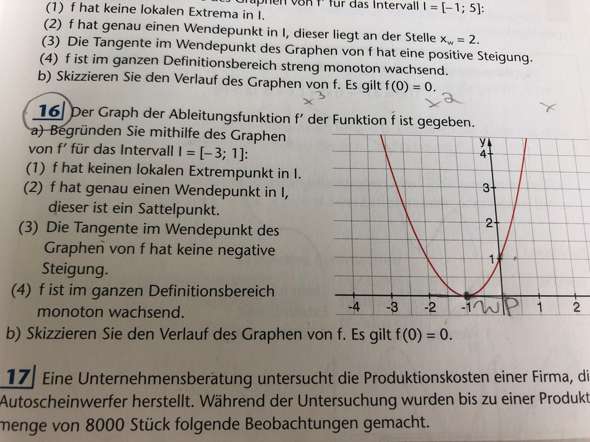
- also zu 16b: du weißt, dass f(x) an der Stelle x=0 durch den Ursprung geht...
- du weißt auch, dass dort die Steigung 1 beträgt.
- du kannst dich nun also ganz ahnungslos stellen und eine Gerade g0 durch den Ursprung mit der Steigung 1 legen.
- dann guckst du wo diese Gerade g0 an der Stelle x=0,5 und x=-0,5 ist...
- dann legst du durch diese beiden Punkte ein Gerade mit der Steigung 2 respektive 0,25...
- brauchst du zu 16a auch Hilfe?
- 16a4: da f' durchweg nicht negativ ist, muss f also monoton steigend sein...
- streng monoton aber nicht, weil f'(-1) nämlich gleich Null zu sein schein... LOL
Könntest du mir bitte auch bei den anderen Aussagen von a) helfen ?
- oh - hast recht...
- das was ich geschrieben hab, ist eine zu scharfe Forderung...
- https://de.wikipedia.org/wiki/Monotone_reelle_Funktion#Ableitungen_als_Monotoniekriterium
2)4) gilt meines Erachtens.
f ' Extremwert und Nullstelle → f Sattelpunkt
f ' im Positiven → f steigt
Wenn f'(x) > 0 steigt der Graph..
Was spricht bei einem Sattelpunkt gegen strenge Monotonie?
Für x1 > x2 gilt f(x1) > f(x2). Mehr braucht man nicht, oder?