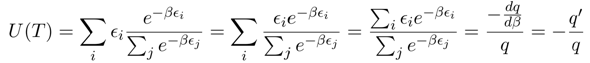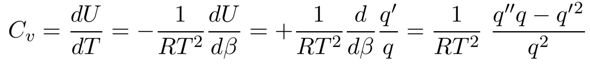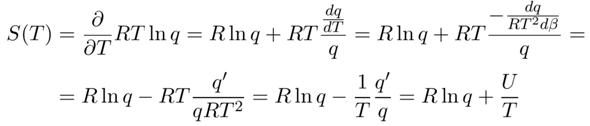Wie werden Zustandsfunktionen in der statistischen Thermodynamik berechnet?

Aus der Zustandssumme q(β) = ∑ exp(−βεᵢ) wobei β=1/(RT). Dazu muß man natürlich wissen, wie die Energieniveaux εᵢ für das System aussehen; oft verwendet man ein Modell, das sich geschlossen summieren oder integrieren läßt, z.B. einen harmoni­schen Oszillator, oder man bastelt sich Zustandssummen aus verschiedenen Model­len zusammen. Irgendein Ausdruck, im schlimmsten Fall eine numerische Tabelle, muß aber bekannt sein.

Im folgenden nehme ich an, daß wir vom kanonischen Ensemble reden, also bei kon­stantem Volumen, konstanter Temperatur und konstanter Teilchenzahl arbeiten. In diesem Fall ist die freie Energie einfach das thermodynamische Potential, F=−RTln(q).

Der Anteil der Moleküle mit Energie εᵢ ist ja einfach exp(−βεᵢ)/q, und die innere En­er­gie bekommt man daher ganz leicht als mit den Besatzungsanteilen gewichtete Sum­me aller Energieniveaux. Dabei bemerkt man, daß der Ausdruck im Zähler genau die Ableitung des Nenners ist, und kommt daher zu einem kompakten Endergebnis (da­bei bedeutet q’ natürlich die Ableitung von q nach β).

Daraus kriegt man sofort die Wärmekapazität als dU/dT, dabei nutzt man aus daß dβ/‍dT=−RT² und daraus dT=−RT²dβ; dann braucht man nur noch die Quotientenregel.

Für die Entropie wissen wir, daß sie das partielle Differential S=−∂F/∂T ist, weil das totale Differential der freien Energie dF = −S dT − p dV lautet. Das setzen wir einfach ein:

Das sieht deutlich schlimmer aus, als es ist: Wir wollen RTln(q) nach T ableiten, und da q selbst temperaturabhängig ist, brauchen wir zuerst die Produktregel, dann die Kettenregel. Dann wechseln wir wieder geschickt von dT nach dβ und bekommen dann wieder das gewöhnlich q’=dq/dβ, das wir mit dem Ausdruck für die innere En­ergie von oben in Verbindung bringen.

(Wenn Du Physiker bist, dann darfst Du natürlich auch die Boltzmannkonstante statt der Gaskonstanten verwenden — Chemiker wie ich denken lieber in Energien pro Mol statt Energien pro Teilchen)

Vorzeichenfehler und andere Schludereien sind wie immer vorbehalten.