Wie lösen?d?

Hey, ich versuche gerade das Thema zu verstehen, weiß aber nicht wie ich smart anfangen soll. Wäre für Tipps sehr dankbar.

Lg

Comments

[Spikeman197]

Gibt es Werte für die Widerstände, oder soll es eine theoretische Lösung sein?

[Pepejulieonsema]

theoretisch

Answer 1

[Ich87309]

So vielleicht

Answer 2

[Spikeman197]

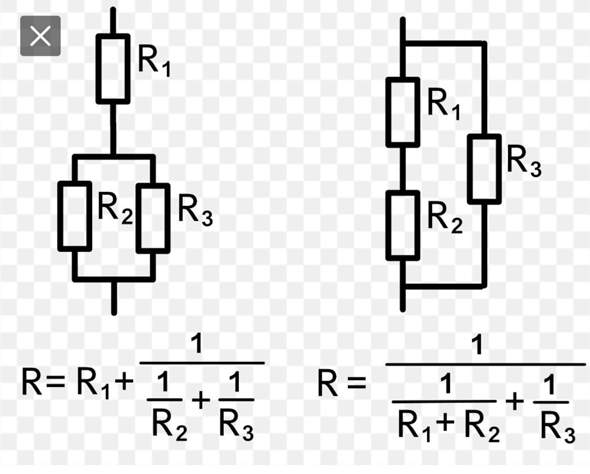
Na, in Reihe addieren sich die Widerstände und parallel addieren sich die Leitwerte, die die Kehrwerte der Widerstände sind....

R(reihe)=Ra+Rb und R(parallel)=(1/Ra +1/Rb)^-1

Da man keine Werte hat, ist es eine ziemliche Schreibarbeit, bzw. Eine Fleißarbeit ist es so oder so. Da gibt es keine Abkürzung...

Comments

[Genuatief]

Du musst glaube ich nicht alles ausrechnen sondern es wird wohl reichen, wenn du beispielsweise für (1) schreibst

Rges= (R1||R2 + R3+R4+5) || R6

😉

[Genuatief]

@Genuatief

Ging an den Fragesteller. Es macht für mich keinen Sinn, diese ganzen Terme auszumultiplizieren...wer hat was davon?

[Spikeman197]

@Genuatief

Um auch noch Spannungen und Stromstärken auszurechnen, die komplette Schaltung halt. wäre halt ne andere Aufgabe...

[Genuatief]

@Spikeman197

Nur mütte man ja nicht alles auf einen Term bringen. Es reicht, die Zwischenergebnisse am Ende einzusetzen:

[Genuatief]

@Genuatief

				Serienschaltungen				Parallelschaltungen	
									
R1	1			R1+R5	6			R2||R6	1.5
R2	2			R2+R6	8			R1||R5	0.833333333
R3	3			R1+R2	3			R3||R4	1.714285714
R4	4			R5+R6	11				
R5	5								
R6	6								
									
									
									
									
Rinf    3.428571429								
Re0	    2.333333333								
Reinf	2.357142857								
Rac	    3.408521303	

Answer 3

[Genuatief]

bei der vierten Aufgabe (was bezeichnest du mit d?)

$R_{2a-2b}=R_{5\ }\left|\right|\ \left(\left(R_1+R_2\right)\left|\right|R_3\left|\right|R_4+R_6\right)$

Das zu einem einzigen Bruchterm auszumultiplizieren bringt nichts, außer dass es mühsam ist.

• R1 und R2 in Serie, das Ergebnis liegt parallel zu R3 und R4
• das Ergebnis liegt in Serie zu R6
• das Ergebnis liegt parallel zu R5

-------------------------------

Von allen Aufgaben ist nur die fünfte Aufgabe bissl tricky:

• Du denkst dir die Widerstände R34 = R3||R4 zumächst weg ("unendlich") und berechnest den Widerstand zwischen a und c:

$R_{ac}^{\infty}\ =\ \left(R_1+R_5\right)\left|\right|\left(R_2+R_6\right)$

• Dann berechnest du den Widerstand, den R34 "sieht", wenn a-c kurzgeschlossen ist:

$R_e^0\ =\ R_2\ \left|\right|R_6+R_1\left|\right|R_5$

• Dann berechnest du den Widerstand, den R34 "sieht", wenn a-c offen ist:

$R_e^{\infty}=\left(R_1+R_2\right)\left|\right|\left(R_5+R_6\right)$

• Der Gesamtwiderstand R(ac) ist dann R(ac, ∞) mal einem Korrekturfaktor, der sich durch das Hinzuschalten von R34 ergibt:

$R_{ac}=\ R_{ac}^{\infty}\cdot\ \frac{R_{34}+R_e^0}{R_{34}+R_e^{\infty}}$

Diese einfache Vorgehensweise durch das vorläufige Herausnehmen eines einzelnen Widerstandes funktioniert immer dann, wenn man die einzelnen Unterschritte und somit den benötigten Korrekturfaktor leicht berechnen kann - dies ist sehr oft der Fall!

https://en.wikipedia.org/wiki/Extra_element_theorem

Beweis hier:

https://www.youtube.com/watch?v=dqpF3SztahU

https://www.youtube.com/watch?v=yo4P3t_OtOc

Es ist zwar überraschend, aber letztendlich nur eine Konsquenz der Linearität der elektrotechnischen Grundgleichungen.

-------------------------------

Es gilt immer: || Rechnung vor + Rechnung