Wie löse ich dieses Extremwertproblem?
Aus einem Kegel mit einem Grundkreisradius von 3cm und einer Höhe von 4cm soll ein Zylinder mit möglichst großem Volumen berechnet werden. Berechnen Sie den Radius dieses Zylinders. Als Tipp wird die Verwendung des Strahlensatz genannt.
Wie berechne ich das?
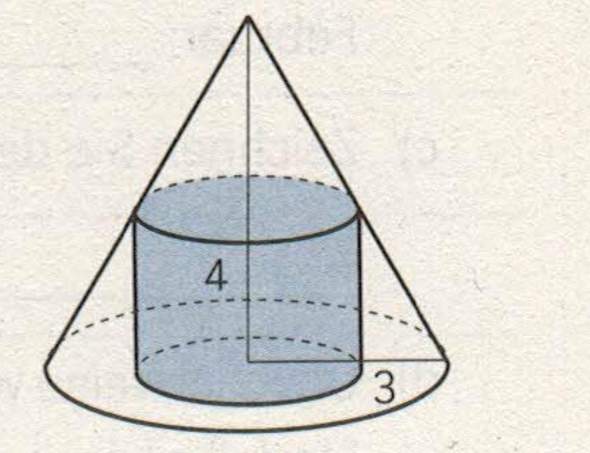
das ist die Skizze
3 Antworten
Mit dem Strahlensatz findest Du das Verhältnis (4-h)/r)=4/3
wobei h die Höhe und r der Radius des Zylinders ist.
Mit V=h*2Pi r^2 hast Du eine zweite Gleichung.
Aus diesem Gleichungssystem baust Du eine Funktion f(V) nach h oder r.
Die Ableitung f'(V) setzt Du gleich 0 und hast den Extremwert.
Also
(4-h)/r=4/3
4-h=4/3 r
h=4-4/3 r (I)
V=h*2 Pi r^2 (II)
(I)->(II) V=(4-4/3 r)*2 Pi r^2
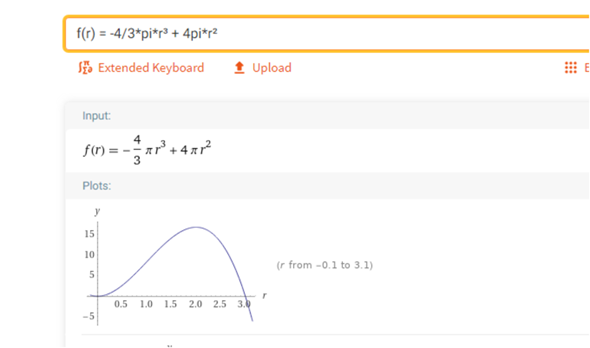
f(V)=8 Pi r^2 - 8/3 Pi r^3
f'(V)= 16 Pi r - 8 Pi r^2 =0 | /8 Pi r
2-r=0
r=2
(I) h=4-4/3 r
h= 4-8/3
h=4/3
Ob ich mich verrechnet habe, habe ich jetzt nicht geprüft. Mach mal noch die Probe. Aber vom Prinzip her sollte das so gehen.
V=pi*r^2*h=max............ist ok ( gehe ich mal von aus ) . Dass dieses "=max" nicht 100% mathekorrekt ist , ist wichtig , aber ich weiß, was du meinst :))
2 Variablen gehen gar nicht , also holt man sich eine Nebenbedingung , um eine Var zu vernichten ............
Hier hilft der Strahlensatz ( mal wieder ) . Jetzt glaub ich mal Florabest
h/r = 4/3 >>>> h = 4/3 * r .......rein in die V-Glg.
V = pi*r^2*4/3*r
= 4pi/3 * r³
Ableiten
3*4pi/3*r² = 4pi*r² ..............das führt in der Tat zu nix , zu r = 0 ...........also stimmt da was nicht.
AHA : Der Strahlensatz war falsch !
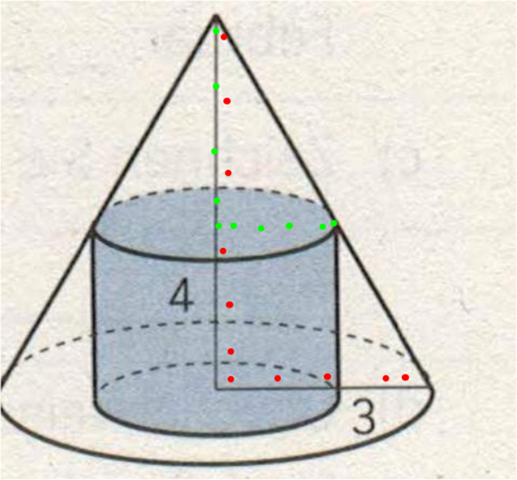
grün zu rot sind die ähnlichen Dreiecke
(4-h)/r = 4/3...................
Nun ist h = - (4/3 * r) + 4
wieder rein in V
pi*r^2*( - (4/3 * r) + 4 )
=
-4/3*pi*r³ + 4pi*r²
ich rechne das nicht vor und durch , aber das führt mit r = 2 dann tatsächlich zu einem Max ..............Danke Roland !
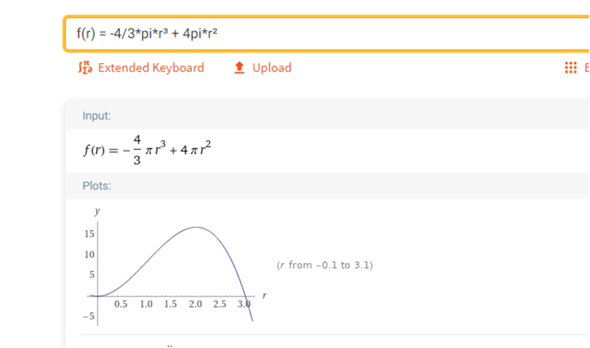
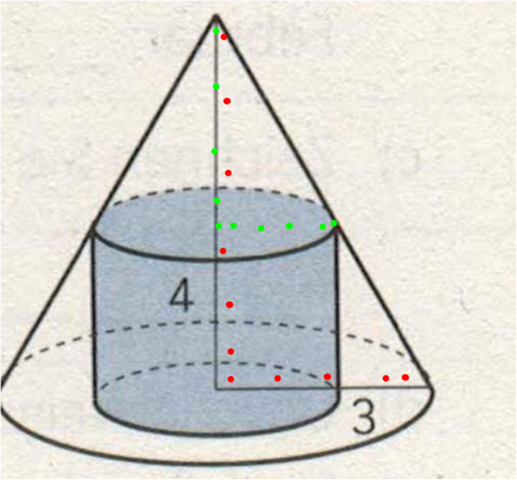
Ich verstehe deine Formulierung nicht.
Wie kann man aus einem Kegel einen Zylinder berechnen?
Du musst schon sagen, was die miteinander zu tun haben sollen.
Ich kann dir jederzeit die Maße eines beliebig großen Zylinders nennen....
Mach eine Skizze,y dann siehst du, wie mit Hilfe der Strahlensätze die Höhen und Radien der beiden Körper voneinander abhängig sind.
Habe ich bereits, komme danach nicht weiter
Ahhh, da ist die Skizze ja schon. Zeichne Radius und Höhe des Zylinders ein. Dann siehst du es. Dann schreibst du die Formel des Volumens des Zylinders hin.
Dann kannst du h durch r oder r durch h ausdrücken (Strahlensatz) und dann mit der Volumenfunktion über Ableitung das Maximum bestimmen.
genau da ist das Problem😅, Hauptbedingung habe ich bereits: V=pi*r^2*h=max. Die Nebenbedingung(en) kriege ich nicht hin.
Ist der Strahlensatz dann die Nebenbedingung?
Kannst es nennen wie du willst.
Der Strahlensatz ist der Strahlensatz. Da kannst du jetzt h durch r ausdrücken und in die Volumenfunktion einsetzen. Dann hast du das Volumen in Abhängigkeit von r.
Dann übliche Extrmwertaufgabe lösen.
Warum sind dir die Worte jetzt so wichtig? Ändert doch nix an der Logik.
irgendwie hab ich jetzt r=0 raus, gebe auf
Ha , jetzt kommt die Retourkutsche zu deiner Aufdeckung meines groben Fehlers neulich bei dem Quaderschlängelband :))
(4-h)/r = 4/3................so sieht das aus !
Oh Mein Gott!!!!
So ein Fehler !!!! ...und das mir!
Lieber Swarley , Halbzeit hat Recht. Ich habe zu grob und zu schnell szf die Skizze geguckt. Der Strhalensatz ist (4-h)/r = 4/3 oder eben (4-h)/4=r/3.
Das mit dem r=0 hast du richtig berechnet. Denn mit Der Ableitungsfunktion ermittelt du ja die Extremwerte. Und bei r=0 ist ein Extremwert - natürlicherweise ist das ein Minimum. Aber das hätte ich dir auch ohne Rechnung sagen können, dass wenn der Zylinder auf einen Strich komprimiert wird, das Volumen sehr sehr klein wird.
Der Zylinder befindet sich in dem Kegel