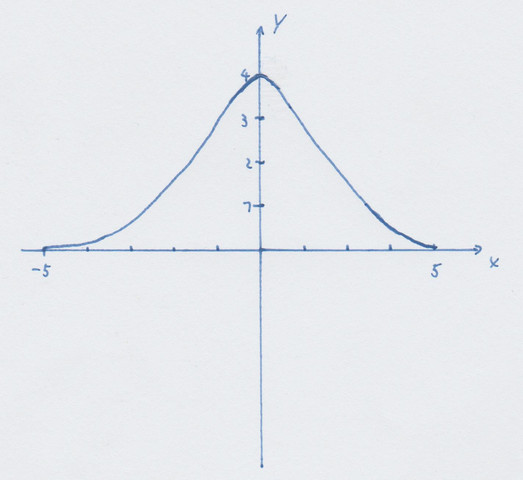
Wie lautet die Funktionsgleichung des abgebildeten Graphen?
Hallo, ich würde gerne wissen wie die Funktionsgleichung des abgebildeten Graphen lautet. Ich würde auch gerne wissen, wie Ihr auf das Ergebnis gekommen seid. (Am besten detailliert erklärt) Bekannt ist, dass der Graph einen Hochpunkt bei HP (0/4) hat und anscheinend wohl gegen 0 geht. Für Antworten wäre ich sehr dankbar.
5 Antworten
Der sieht aus wie die Gaußfunktion:
f(x) = K*e^(-a*x² )
http://www.wolframalpha.com/input/?i=f(x)+%3D+e%5E(-x%C2%B2+)
Mit Maximum bei x = 0 und f(0) = 4 folgt:
K = 4
--> f(x) = 4*e^(-ax²)
und mit f(5) = ca. 0.01 folgern wir:
0.01 = 4*e^(-a*25) II /4 II log(...) <--- Log zur Basis e
log(0.01/4) = -(a)*25 II *(-1/25)
log(4/0.01)/25 = ca. 0.24 = a
Somit erhalten wir:
f(x) = 4*e^(-0.24*x²)
http://www.wolframalpha.com/input/?i=f(x)+%3D+4*e%5E(-0.24*x%C2%B2)
Dabei ist alles obige nur eine Schätzung. Man könnte beliebig viele Funktionen finden, die ein ähnliches Aussehen besitzten wie der Graph deiner Skizze. Der Hochpunkt und der "ungeaue" graphische Verlauf reichen da leider nicht aus.
Sieht für mich ein wenig aus wie die Dichtefunktion der Normalverteilung:
1/Wurzel(2*pi*Sigma) * e^(-x/(2*Sigma²))
kann aber auch vieles andere sein...
Hallo,
f(x)=[25/(2*Pi)]*e^(-0,18x²) sieht Deiner Kurve recht ähnlich, finde ich.
Siehe Anhang.
Herzliche Grüße,
Willy

ne Glockenkurve?
http://www.mathematische-basteleien.de/glockenkurve.htm
sowas gab's früher auf nem Geldschein (10DEM, glaub' ich)...
Stimmt - der (neuere) 10-DM-Schein war C. F. Gauß gewidmet. Dieser Mathematiker hat u. a. die Ausgleichsrechnung "erfunden" und dabei die Normalverteilung entdeckt.
Okay, wenn die anderen auf eine Exponentialfunktion (Gaußsche Glockenkurve) tippen, biete ich mal eine Alternative. Für den Fall, dass Ihr gebrochen rationale Funktionen hattet, könnte es z.B. auch
4
f(x) = -------
x² +1
sein.
Aber wie schon angedeutet: da gibt es wohl unendlich viele Möglichkeiten.

Erstmal danke für die Antwort!
Bei
log(0.01/4) = -(a)*25 II *(-1/25)
log(4/0.01)/25 = ca. 0.24 = a
Warum werden Zähler und Nenner im Bruch vertauscht?