Wie lässt sich eine if-else Bedingung mathematisch darstellen?
Es soll eine Kennziffer berechnet werden. Die Anwendung der Formel zur Berechnung der Kennziffer hängt davon ab, ob d<2 oder d>2. D. h. es gibt zwei Varianten, wobei nur eine je nach Szenario angewandt werden darf.
Übersetzt soll die Formel dann lauten:
Kenngröße = d*p+[...], falls d<2
Kenngröße = d*a+[...], falls d>2
Die mathematische Notation hier formal korrekt abzubilden ist vermutlich schwer, deshalb bin ich schon für einen Link zur korrekten Notation dankbar.
8 Antworten
Am gängigsten ist es, wenn du es mit einer geschwungenen Klammer schreibst wie in dem beigefügten Bild- damit du es richtig siehst musst du drauf klicken. (Meistens wird deine Kenngröße, da die dann ja von d abhängig ist als eine Funktion f(d) gesehen) Es wäre aber genauso korrekt wenn du eine Fallunterscheidung machst.
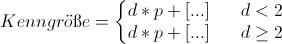
Ja, so notiert es auch
Du kannst es in logischer Notation als Aussage hinschreiben. Die fehlende Information bezüglich des Falles, daß d = 2 ist, muß eingesetzt werden
d<2 ∧ d*p+[...] ∨ d=2 ∧ [?] ∨ d>2 ∧ d*a+[...]
∨ ist das Symbol für logische Disjunktion. Es bedeutet "oder". (Ähnelt dem Buchstaben v, ist aber kein v.)
∧ist das Symbol für logische Konjunktion. Es bedeutet "und".
Das ∧ hat Vorrang vor dem ∨.
Halt, ich habe geschludert. Habe vergessen, den Ventilator anzuschalten und das ist nun die Folge. Berichtigung folgt:
Es soll ja eine Aussage sein, und zwar eine Aussage über den Wert der Kenngröße. (Ich nenne sie K.)
K ist definiert durch die Aussage:
d<2 ∧ K=d*p+[...]
∨ d=2 ∧ K=?
∨ d>2 ∧ K=d*a+[...]
Naja... *hüstel*... mittels der Signumfunktion und dem Kronecker-Delta geht das schon... ;-)))
KroneckerDelta_1,sgn(d-2) ist 1 für d>2 und 0 sonst. Damit multiplizierst du also den einen Fall der Berechnung. Den Fall <=2 dann eben mit 1-(KroneckerDelta_1,sgn(d-2)).
Tataa, geschlossene Formel. Aber schon arg gefrickelt... ;-)))
http://de.wikipedia.org/wiki/Kronecker-Delta
de.wikipedia.org/wiki/Vorzeichenfunktion
Auch wenn das formal "stimmt", bekomme ich da Bauchschmerzen. Die Heaviside-Funktion stammt aus einem vollkommen anderen Kontext, der Nachrichten- und Regelungstechnik (die jetzige Generation würde ungeniert sagen: der "Analogtechnik"), wo man Netzwerkantworten auf Vorgänge wie die Sprungfunktion errechnet, indem man ihre Differentialgleichungssysteme, anstatt sie in Zeitkoordinaten zu lösen, durch Fourier- oder Laplace-Transformation in Frequenzkoordinaten abbildet. Zu Sachen wie stückweise definierten Formeln bei der Berechnung von Kennziffern sehe ich da keine methodische Beziehung. Es fühlt sich für mich an, wie die Bohrmaschine zum Einschlagen von Nägeln zu benutzen. Schwer genug dafür ist sie schon... >:-)
Nunja... eine Fallunterscheidung mit geschweifter Klammer ist sicher üblicher und auch übersichtlicher. Aber er wollte es halt so, warum auch immer. ;-))
Mit "Die mathematische Notation hier formal korrekt abzubilden ist vermutlich schwer" meinte ich das limitierte Layout dieser Seite. Ich kann mir nämlich nicht vorstellen wie
KroneckerDelta_1,sgn(d-2)
aussehen soll. Ich versteh auch nicht ganz warum hier was multipliziert wird.
Schreibe ich gemäß dem Wikipedia-Definitionsmuster anstelle der 1 und der 0 einfach die beiden alternativen Formeln jeweils mit der Bedingung dahinter?
Das Kronecker-Delta ist der kleine griechische Buchstabe Delta mit zwei Indizes. Die Heaviside-Funktion wäre aber, wie gesagt, eleganter (braucht keine Signum-Funktion).
Multipliziert wird, weil meine Konstruktion jeweils in einem Gültigkeitsbereich den Wert 1 liefert (also deinen damit multiplizierten Term), und an allen anderen Stellen 0 (also nichts). Das ganze wird addiert mit dem Ergebnis des komplementären Bereichs.
Also mittels Heaviside-Funktion (großes Theta oder auch H; letzteres ist hier wohl besser):
H(d-2) * (d*a+[...]) + (1-H(d-2)) * (d*p+[...])
Liefert genau
- d*a+[...], falls d>=2
- d*p+[...], falls d<2
Ich würde das mit einer großen geschweiften Klammer aufschreiben. So wurde das auch schon öfter in Vorlesungen geschrieben.
Siehe hier http://mo.mathematik.uni-stuttgart.de/kurse/kurs44/seite25.html ganz unten auf der Seite.
Ouwah! Es geht noch eleganter:
http://de.wikipedia.org/wiki/Heaviside-Funktion