Wie kann man den Sinussatz in einem Trapez anwenden?
Ich habe a,b,c und alpha in einem Trapez ABCD gegeben. Wie kann ich die restlichen Winkel und d mit dem Sinussatz berechnen?
3 Antworten
Ein Trapez kann man auf unterschiedliche Arten in Dreiecke unterteilen. In allen diesen Dreiecken kann man den Sinus- und den Cosinus-Satz (und den Winkelsummensatz etc.) anwenden.
Erstelle eine Skizze von einem Trapez. Verschiebe die Seite b (rechte Seite) parallel soweit, dass die Grundseite die Länge a - c hat. Jetzt hast Du ein Dreieck mit der Grundseite a - c, der Seite b (gegenüber von α) und dem Winkel α.
Es gilt: b / sin(α) = (a - c) / sin(γ)
Bestimme Winkel γ.
Mittels Winkelsumme im Dreieck erhältst Du Winkel β. Das ist wegen der Parallelverschiebung gleichzeitig der rechte untere Winkel im Trapez.
...
Ich habe den Dreieckswinkel in D γ genannt. Dieser ist nicht zu verwechseln mit den Winkeln γ und δ im Trapez. β_Trapez ist dann, wie angegeben, 180° - α_Trapez_Dreieck - γ_Dreieck.
Ich gehe von der folgenden Beschriftung aus:
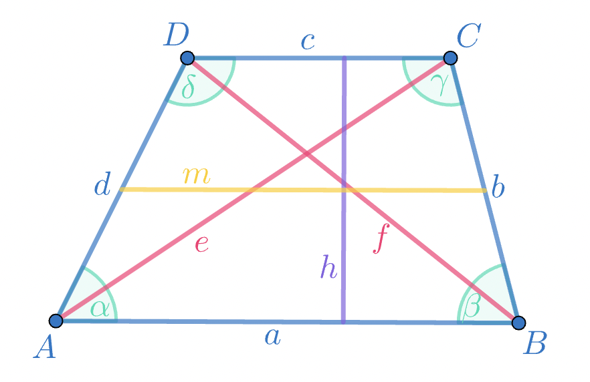
Wenn alpha gegeben ist, ist auch delta gegeben, weil alpha + delta = 180°.
Nun verschiebst du b parallel durch D, so dass ein Parallelogramm BCDX entsteht. Du denkst dieses Parallelogramm abgeschnitten, so dass ein Dreieck AXD verbleibt. In diesem Dreieck kannst du den Sinussatz anwenden. Es gilt:
b/sin(alpha) = (a - c) / sin(delta-beta). Damit kannst du beta ausrechnen.
Weiter gilt: 180°-beta=gamma.
d kriegst du dann selber raus.
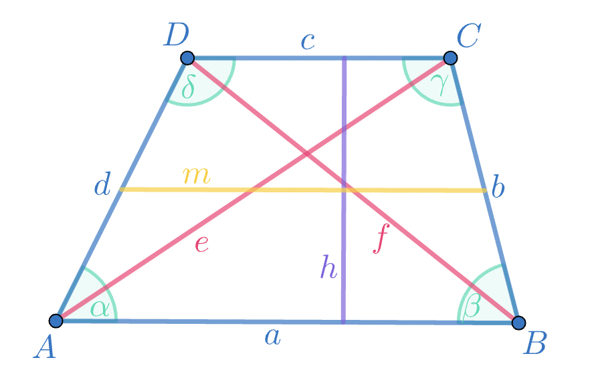
Mir scheint, deine Formel ist falsch.
Es gilt: b / sin(alpha) = (a - c) / sin(delta-beta).