Wie gibt man eine Stammfunktion in Geogebra ein oder wie berechnet man das unbestimmte Integral mit Geogebra?
Hallihallo!
Frage befindet sich oben und die Aufgabenstellung steht auf dem Foto im Anhang! Wie kann ich diese Aufgaben mit Geogebra lösen und wie kann ich diese händisch machen? Bitte hilft mir, es ist wirklich sehr dringend! DANKESCHÖN
Kuss eure Isa

2 Antworten
Mit Geogebra kannst Du das nicht lösen, da GG nicht mit einem allgemeinen a arbeitet, sondern immer einen konkreten Wert verlangt.
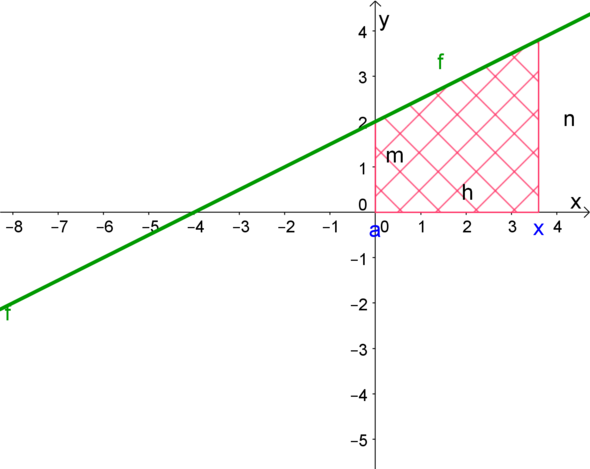
Zur Veranschaulichung habe ich mal die Funktion 58c gezeichnet. Da siehst Du das Trapez gut. (Ich habe absichtlich andere Buchstaben als in der Formel benutzt, da a schon als Integrationsgrenze vergeben ist.)
Für die Fläche gilt: A = (m+n)/2 · h = [f(a) + f(x)] / 2 · (x-a)
Du setzt also den konkreten Funktionsterm sowie den Wert für a ein und rechnest das Ganze aus. Dabei kommt, wie schon in der Aufgabe angegeben, ein Term für F(x) heraus, also eine Funktion. Deren Graph sollst Du anschließend zeichnen. F(x) gibt Dir also den Flächeninhalt Deines Trapezes in Abhängigkeit von der rechten Intervallgrenze x an.
Bei anderen Aufgaben ist Dein Trapez übrigens ein Dreieck (da f(a) = 0).
Ich wüsste nicht wie man das da berechnet oder als Integral darstellt. Du kannst das mit WolframAlpha machen oder einfach ausrechnen und bei Geogebra eingeben,dann hast dus ja auch dargestellt.
&Wie rechnet man das richtig aus? Könntest du mir das bitte erklären? :)
Es gilt als Regel: ax^n 'aufgeleitet' ist gleich (a/(n+1))*x^(n+1). wenn du also eine funktion f(x)=x^2+3x hast ist das unbestimmte integral F(x)=(1/3)x^3+(3/2)x^2. Willst du jetzt das Integral von a bis b berechnen ist das = F(b)-F(a).