Wie geht das (Mathehausaufgaben)?
Hallo Leute,
Ich war krank und muss diese Arbeitsaufträge machen und verstehe diese Aufgabe nicht ( wie kann man den Flächeninhalt davon berechnen?).
Kann mir jemand diese Aufgabe erklären und wenn es geht anhand von zum Beispiel a)?
Lg
9 Antworten
Hey, dabei geht es um den Satz des Pythagoras, den Kathetensatz und Höhensatz, soweit ich das richtig sehe. Lies das doch mal nach, es ist ziemlich einfach, weil immer von denselben Variablen die Rede ist und du die Werte, die gegeben sind, dann einfach auf sie übertragen kannst
Pythagoras
Bei a hast du die Fläche eine Kathete direkt angegeben, die Länge der Hypothenuse hast du auch, da sollte sich die Fläche der zweiten Kathete doch berechen lassen
a² + b² = c²
b² = 15 cm², c = 60 mm
wenn Du ein rechtwinkliges Dreieck hast, wo a und b die Länge der Katheten sind und c die Länge der Hypothenuse, dann gilt:
a^2 + b^2 = c^2
Nun musst Du in jeder Teilaufgabe das einsetzen, was Du gegeben hast und die entsprechende Unbekannte ausrechnen.
Beispiel a)
gegeben ist b^2 = 15 cm^2 und c = 6cm
also a^2 + 15 cm^2= 36 cm^2.
Nun kannst Du a^2 ausrechnen.
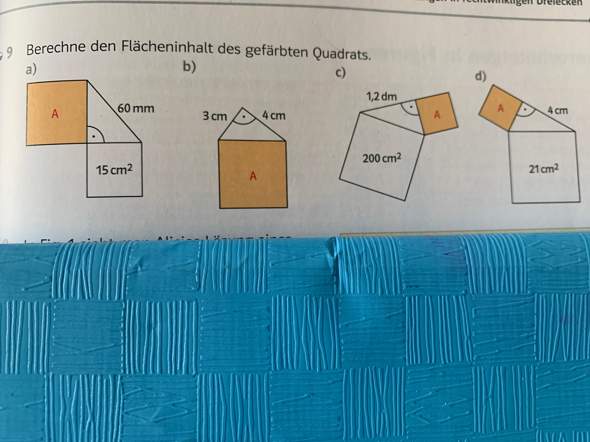
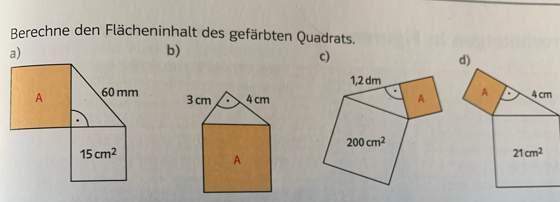
a) Wie groß ist die Kantenlänge x eines Quadrates, dessen Fläche A1 (= 15cm²) ist?
x = √A1
Wie groß ist die Kathete K1 eines rechtwinkligen Dreiecks, wenn die Hypotenuse H (= 60mm) und die andere Kathete K2 (= x) ist?
Pythagoras: H² = K1² + K2²
Wie groß ist die Fläche des Quadrates mit der Kantenlänge K1?
Grundsätzlich: Wenn man etwas nicht kann, macht man erst mal das, was man kann.
Du kannst dir erstmal in Erinnerung rufen: Die Summe der Quadrate über den Katheten ist gleich dem Quadrat über der Hypothenuse.
Zu Aufgabe a): Du kannst erst mal die 60mm in cm umwandeln.
Du kannst das Quadrat über der 60mm-Seite berechnen.
Zu b) Du kannst die Fläche jedes einzelnen Kathetenquadrates ausrechnen.
Zu c) Du kannst erst mal die 1,2dm in cm umwandeln.
Jetzt kannst du die Quadratfläche über dieser Seite ausrechnen.
Zu d) genauso zu bearbeiten wie c)
Und dann überlegst du dir, wie du weiter arbeitest.
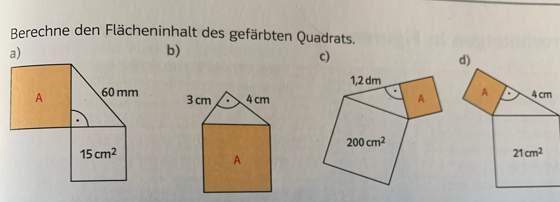
Aber warum wird aus 6cm 36cm^2