Wie erkläre ich das am besten?
Hiii, wie kann ich den Vorgang bei Aufgabe 9 am besten erklären?

3 Antworten
Hallo,
mit dem Satz des Pythagoras. Da eine Kathete immer gleich 1 ist und die Wurzel aus 1 auch 1, ergibt sich die längste Seite jeweils aus der vorigen längsten Seite plus 1.
Das erste Dreieck ist gleichschenklig rechtwinklig mit zwei Katheten der Länge 1.
Dann gilt: c²=1²+1²=2, wobei c hier immer die längste Seite, also die Hypotenuse ist.
Das nächste Dreieck hat wieder die 1 als Kathete, während die andere die Hypotenuse des Dreiecks davor ist, also Wurzel (2). Wurzel (2) zum Quadrat ist natürlich 2 und 1 zum Quadrat ist immer 1.
Für das nächste Dreieck gilt daher: Wurzel (2) zum Quadrat plus 1 gleich 2+1=3.
Das ist das Quadrat der neuen Hypotenuse, deren Länge damit die Wurzel aus 3 ist.
Dann kommt Wurzel (4), Wurzel (5) usw.
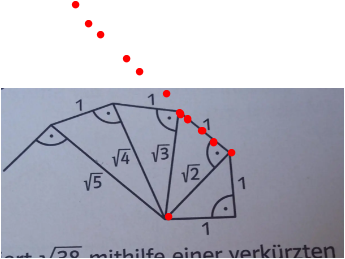
Möchtest Du die Wurzel aus 38 konstruieren, brauchst Du ein Dreieck mit Wurzel (37) als Hypotenuse. Da die Wurzel aus 37 aber eine irrationale Zahl ist, fängst Du bei dem Dreieck davor an mit der Wurzel aus 36. Da 36 eine Quadratzahl ist, weißt Du, daß deren Wurzel die 6 ist. Du zeichnest eine 6 cm lange Linie, fügst im rechten Winkel dazu eine Linie von 1 cm Länge an und verbindest die beiden Enden.
Dann gilt wieder: 6²+1²=37. Das ist das Quadrat der neuen Hypotenuse, die demnach die Wurzel aus 37 als Länge besitzt.
Nun hast Du die Wurzel aus 37, fügst wieder die Linie mit der Länge 1 im rechten Winkel an und erhältst als Verbindung der Enden die Hypotenuse mit der Länge Wurzel (38).
Du mußt also nicht jedesmal bei 1 anfangen, sondern bei der nächstniedrigeren Quadratzahl. Das ist mit der verkürzten Schnecke gemeint.
Über einen Thaleskreis könntest Du auch das nächstniedrigere Dreieck konstruieren, was praktisch ist, wenn Du etwa die Wurzel aus 48 suchst.
Dann fängst Du nicht bei Wurzel (36) an, sondern bei Wurzel (49)=7 und arbeitest Dich ein Dreieck nach unten.
Herzliche Grüße,
Willy
gezeichnet wurde zuerst ganz rechts das Dreieck mit 1 und 1 . Wegen Pythagoras ist die Hypotenuse nun wurzel ( 1² + 1² ) = wurz(2) = w(2)

dann ein rechter Winkel mit Schenkellänge 1 an diese w(2)_Hypotenuse , so entsteht w(3)
für w(38) dann gelten w(38) = ( ( w(5) )² + x² ) = ( 5 + x² ) . Dann müsste x² = 33 sein . Das kriegt man nicht hin .
Also "tricksen"
nutze die w(2) , verlängere die 1 auf 6

dann hat man
( (w(2)² + 6² ) = ( 2 + 36 ) = 38 und die Hypo ist nun w(38)
9)
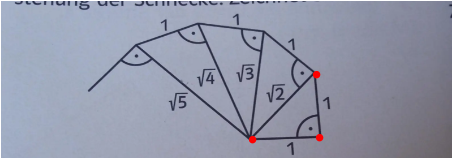
Zur Formung einer Schnecke werden rechwinkelige Dreiecke aneinander gereiht. Eine der beiden Katheden ist immer 1 LE lang.
Beim Übergang vom Dreieck (n) zu Dreieck (n+1) wird die Hypothenuse von Dreieck (n) zur Kathede von Dreieck (n+1).
Die Länge der Hypothenuse des kleinsten Dreiecks beträgt √(1+1) = √(2)
Die Länge der Hypothenuse des nachfolgenden Dreiecks beträgt √(2+1) = √(3)
Die Länge der Hypothenuse des nachfolgenden Dreiecks beträgt √(3+1) = √(4)
usw.
Das Dreieck mit einer Hypothenuse von √(38) hat dann die Kathede √(37).
Zur Konstruktion folgender Vorschlag. Die Länge √(4) drei mal länger machen (mit einem Zirkel). Dann hat man 3*√(4) = √(36). Von da aus kann man sich mit obigem Schema bis √(38) vorhangeln.
mein Ansatz kommt mir zu einfach vor , sodass er falsch sein könnte
im Dreieck mit wurz(2) die 1 auf 6 bringen