Wie diese Bruchtermgleichung lösen?
Ich verstehe nicht, wie man diese Bruchgleichung lösen soll.
4-x^2 ist ja durch (2-x)(2+x) entstanden, aber in den anderen Nennern kommt kein negatives x vor und auser in x-2 kommt keine negative 2 vor.
Wie löse ich diese Aufgabe?
Danke für Hilfe.
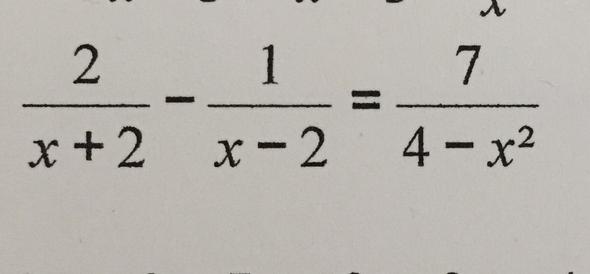
6 Antworten
Bruchgleichungen löse ich immer so, dass ich erst einmal alle Brüche gleichnamig mache. Dazu bennötige ich den Hauptnenner, den ich dadurch bekomme, dass ich alle vorhandenen Nenner so weit wie möglich faktorisiere; dann sehe ich sämtliche Faktoren, aus denen der HN besteht:
x+2 lässt sich nicht zerlegen; ebenso x-2.
4 - x² (3. Binom) = (2-x)(2+x) = -(x-2)(x+2)
Somit besteht der HN aus den Faktoren (x+2), (x-2) und (-1).
Nun erweiterst Du sämtliche Brüche mit den fehlenden Faktoren, multiplizierst mit dem HN (dadurch fallen alle Nenner weg) und kannst nun "normal" auflösen.
Lösung: x = -1.
Wenn du bei den linken Brüchen den Hauptnenner gebildet hast, kannst du rechts und links die Nenner kürzen und du hast nur eine ganze Gleichung!
2(x-2) - x+2 = 7
und x ausrechnen wirst du ja noch hinbekommen!
Den ersten Term musst du mit 2-x erweitern. Den zweiten Term mit -1·(2+x). (bzw. erst mit -1, dann mit 2+x. Ist vielleicht einfacher zu verstehen)
also bei dem bruch 2/x+2 würde ich die 2 streichen
du musst kreuzprodukt und bionomische formel anwenden