Lösungsweg Mathe?
Wir haben momentan Cosinus, Sinus und Tangens im Mathe Unterricht und ich verstehe nicht wie ich die Aufgaben lösen soll.
Ich möchte hier auch nicht nach den Lösungen fragen, sondern nur den Weg zur Lösung verstehen.
(Aufgaben: 4, 5, 18, 12a und 13a)


2 Antworten
6 Schritte auf dem Weg zum ultimativen Erfolg vorweg
.
1)
finde das rechtwinkelige Dreieck oder "konstruiere" es
2)
finde den rechten Winkel
3)
ihm gegenüber ist die Hypotenuse
4)
die beiden anderen Seiten sind die Katheten
(was Gegen- , was Ankathete ist steht noch NICHT fest)
5)
Welcher Winkel ist gegeben, welche Seite ist gegeben ?
6)
Danach richtet es sich , ob man Sin, Cos oder Tan einsetzen kann
.
.
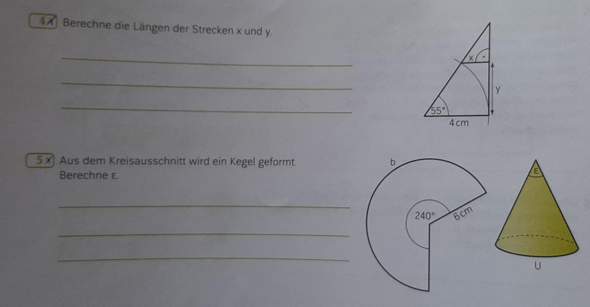
Aufgabe 4
.
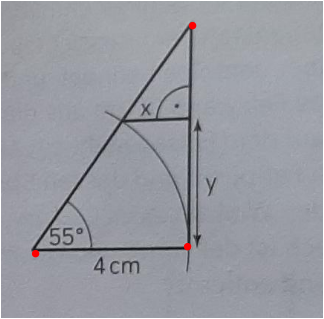
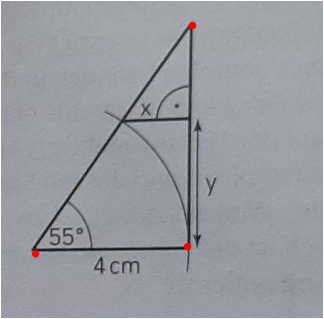
Tricky !
Gesucht x und y , aber direkt lassen sie sich nicht berechnen . Aber mit
???(55) = ganze Senkrechte / 4
die ganze Senkrechte (gS)
.
Nun mit
???(55) = gS/Hypotenuse
die Hypotenuse H
.
Nun mit H minus 4 (beachte den Kreisbogen) die Hypotenuse HkD im oberen kleinen Dreieck
.
Extra Trick :
Der Winkel dort wo das x steht , ist auch 55 ( Stufenwinkel )
.
Nun mit
sin(55) = Seite/HkD
und
cos(55) = Seite/HkD
die anderen beiden Seiten im kleinen Dreieck ( eine davon ist x )
.
jetzt ist auch y kein Problem mehr
.
Bei Sinus, Cosinus und Tangens brauchst du (Anfänger) immer ein Dreieck mit rechtem Winkel.
Dann gibt es einen weiteren Winkel und drei Kante.
Die Kanten sind:
- Ankathete: die eine der kurzeren, die am Winkel liegt
- Gegenkathete: die eine der Kürzeren, die gegenüber von Winkel liegt
- Hypothenuse: die lange Seite, gegenüber vom Rechten Winkel
Nun musst du sehen, was gegeben hast und wo der Winkel liegt.
Mit einer der drei Funktionen bekommst du das Verhältnis zwischen den Längen der Seitenkanten.
Die Idee dahinter ist, dass die Winkel gleich bleiben, wenn du jede Seitenkante mit einem Faktor multiplizierst, beispielsweise verdoppelst.