Wie bestimme ich eine Scheitelpunktform aus folgendem Funktionsterm?
x^4 + 2.5x^2 - 3.5
5 Antworten
Das ist eine ganzrationale Funktion 4. Grades, da gibt es keine Scheitelpunktform - das ganze funktioniert nur bei quadratischen Funktionen.
Jedoch kannst Du die Funktion substituieren, indem Du x² durch eine andere Variable wie u ersetzt, sodass eine quadratische Funktion entsteht, aus der Du die Scheitelpunktform bilden kannst.
Das ganze habe ich Dir unten mal veranschaulicht.
Die Substitution wird zum Beispiel dann angewandt, wenn die Nullstellen der Funktion vierten Grades bestimmt werden sollen, man sich aber im Rechenweg einfach halten möchte - und von quadratischen Funktionen lassen sich die Nullstellen eben einfacher bestimmen als von quartischen Funktionen.
Natürlich müsste anschließend noch durch Wurzelziehen auf die tatsächlichen Nullstellen der quartischen Funktion geschlossen werden - aber wie Substitution genau funktioniert, habe ich Dir ja einer Deiner letzten Fragen schon erklärt.
LG Willibergi
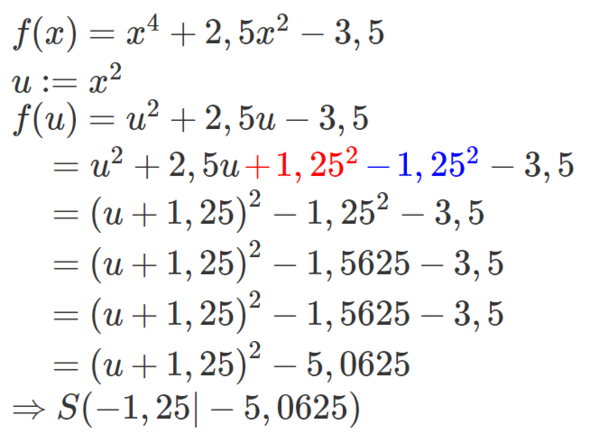
Absolut richtig. Da ist mir tatsächlich ein kleiner Formalitätenfehler unterlaufen. Vielen Dank für den Hinweis.
Und muss dann nicht noch eine Resubstitution durchgeführt werden, weswegen die Scheitelpunkte im C liegen?
Denn u = 1.25 => x² = -1.25 => x1, x2 = i*Wurzel(1.25)
Im Normalfall geht das nicht
f(x)=x⁴+2,5*x²-3,5 Minimum bei xmin=0 und ymin=-3,5
Nullstellen bei x1=-1 und x2=1
habe ich mit meinen Graphikrechner (GTR,Casio) ermittelt
Der Graph sieh wie eine nach oben offenen Parabel aus.
Scheitelpunktform der Parabel f(x)=a*(x-xs)^2+ys
man könnte nun für ys=-3,5 und xs=0 einsetzen
ergibt f(x)=a*x^2-3,5 mit x1=-1 und x2=1 ergibt
0=a*1^2-3,5 ist a=3,5/1^2=3,5
f(x)=3,5*x²-3,5 diese Parabel hätte die gleichen Werte bei x=0 y=-3,5 und die beiden Nullstellen wären gleich
Setze y=x²
x^4+2,5x²-3,5=y²+2,5y-3,5=(y+1,25)²-(1,25)²-3,5
=(y+1,25)²-5,0625=(x²+1,25)²-5,0625
Was oder wie lernt ihr heute in der Schule?
Diese Funktion ist wie ein offenes Buch. Ich würde prüfen, ob der Scheitelpunkt bei 2,5 | -3,5 liegt.
Ich würde prüfen, ob der Scheitelpunkt bei 2,5 | -3,5 liegt.
Das ist sicherlich nicht der Fall.
Einklammern
Die erste Zahl in dee Klammer ist der x wert die zweite Zahl der y
Lade dir PhotoMath runter
Kleine Anmerkung:
Wenn Du eine Funktion f mit
f(x) = x⁴ + 2,5 x² - 3,5
betrachtest und u = x² setzt, so ist genau genommen
f(u) = u⁴ + 2,5 u² - 3,5 = x⁸ + 2,5 x⁴ - 3,5.
Stattdessen wäre es formal korrekter eine neue Funktion g mit
g(u) = u² + 2,5 u - 3,5
zu betrachten, so dass dann g(u) = g(x²) = f(x) ist.