Wie berechne ich die Nullstellen folgender Funktion?
Hallo,
Ich soll die Nullstellen folgender Funktion berechnen:
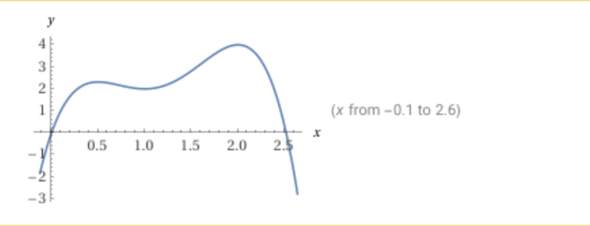
f(x)= -3x^4 + 14x^3 - 21x^2 + 12x
Ich habe zunächst die Ableitung davon gebildet und bin auf folgende Funktion gekommen: f´(x)= -12x^3 + 42x^2 - 42x + 12
Das ganze habe ich dann ausgeklammert:
x ( -12x^2 + 42x - 42) +12
ich wollte dann die pq-Formel für die Werte, diemin der Klammer stehen, anwenden, doch weiß ich nicht, was dann mit der 12 passiert.
Gint es noch einen anderen Weg die Nullstellen herauszufinden?
danke schonmal im Voraus
4 Antworten
Wozu bildest Du die Ableitungsfunktion, um Nullstellen zu berechnen? Die erste Nullstelle findest Du bei x = 0 durch Ausklammern des Linearfaktors -3x.
f(x) = -3x * (x^3 - 14/3 x^2 + 7 x - 4)
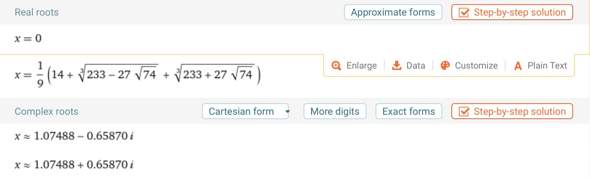
Für das kubische Polynom liegt mindestens eine weitere reelle Nullstelle vor. Man kann versuchen, diese Nullstelle zu „erraten“, indem man als Linearfaktor alle ganzzahligen Teiler des absoluten Gliedes durchprobiert. Dies führt nicht immer, wie auch hier, zum Ziel. Ansonsten kann man die Nullstellen mit Hilfe der Formel von Cardano ermitteln. Zwei davon sind in diesem Falle komplex. Ich denke, Du hast Dich bei der Aufgabe bei einem der Koeffizienten des Polynoms vertan - ich tippe mal auf den kubischen Term, da ansonsten alle Koeffizienten durch 3 teilbar sind…😀


Hallo,
die pq-Formel funktioniert bei kubischen Funktionen nicht. Da bräuchtest Du schon die Formel von Cardano, die neben zwei komplex konjugierten Nullstellen als weitere reelle Nullstelle noch 2,516904355 ausspuckt.
Das bei Schülern übliche Verfahren - eine Nullstelle raten, dann durch Polynomdivision den Grad der Gleichung verringern - klappt hier nicht.
Entweder Du freundest Dich mit Cardano an oder Du nutzt ein numerisches Verfahren wie das von Newton oder Du läßt den Taschenrechner ran.
Herzliche Grüße,
Willy
Wieso denn die Ableitung?
Die brauchst du für die Nullstellen gar nicht.
Um Nullstellen zu berechnen, setzt du einfach f(x) = 0.
Da in jedem Summand ein x vorkommt, könntest du theoretisch die Nullregel (Nullproduktregel) anwenden – aber das hilft dir hier nicht wirklich weiter, weil du dann bei einer kubischen Gleichung landest.
Normalerweise löst man sowas bei biquadratischen Funktionen über Substitution – aber auch das funktioniert hier nicht, weil die Funktion asymmetrisch ist.
Wenn du so einen weißen Casio-Taschenrechner hast:
Geh auf Gleichungen → Polynome → Grad 4, gib die Koeffizienten ein, und der rechnet’s dir aus.
Ohne Taschenrechner bleibt dir als Schüler leider nicht viel anderes übrig – außer raten, schätzen oder grafisch lösen.
Warum berechnest du für die Nullstellen die Ableitung?
Die Nullstellen der Ableitung sind (i.d.R) Extrema und NICHT Nullstellen der eigentlichen Funktion.
Die erste Nullstelle findest du durch ausklammern von x
Besser -3x ausklammern. Dann wird es einfacher, das Restpolynom auf eine weitere Nullstelle zu untersuchen.