Wie aus der Normalform einen Graphen Zeichnen?
Ich lerne gerade Quadratische Funktionen und stecke bei einer Aufgabe fest, die lautet:
y= x² + 3x -4
Zeichnen Sie den Graphen mithilfe einer Wertetabelle mit 7 Wertepaaren, lesen sie die Nullstellen ab. <
Kann man aus dieser Form überhaupt einen Graphen zeichnen oder geht es nur mit der Scheitelpunktform? Ich weiß nur, wie es mit der Scheitelpunktform geht und wie man die Normalform in diese umwandelt haben wir nie gelernt..
Und kann man aus der oben genannten Funktion die Nullstellen oder den y-Achsenabschnitt herauslesen? Wenn ja, wie?
Bin dankbar für jede Antwort! :)
5 Antworten
Du musst x - Werte einsetzten und dann damit die y-Koordinate bestimmen.
Machen wir ein Beispiel.
Wir setzten in die Funktion y = x² + 3x - 4 die x-Koordinate x = 0 ein.
y = 0² + 3*0 - 4
y = - 4
Noch besser wenn man es so aufschreibt:
f(0) = -4
Man fängt aber immer mit y in der Schule an. Wenn ihr das mit f(x) bzw. hier f(0) noch nicht gemacht habt, dann schreibe einfach weiterhin y!
Das, was wir berechnet haben heißt jetzt, dass bei der x-Koordinate x = 0 der Graph die y-Koordinate y = -4 hat.
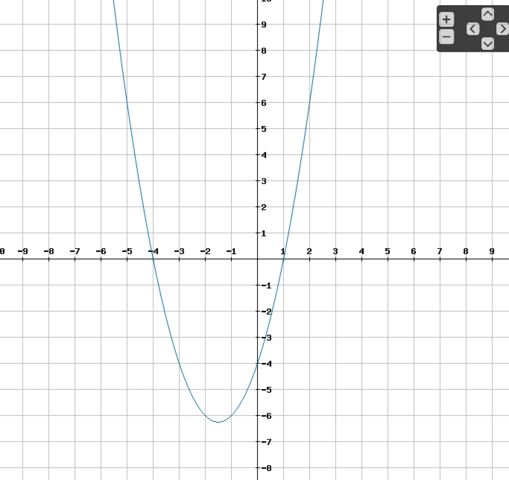
Im Bild siehst du das noch einmal gut. Dort schneidet der Graph genau die y-Achse bei y = -4.
Der Graph geht also durch den Punkt P( 0 | -4).
Genauso sollst du das weiter mit insgesamt 7 Werten machen, also noch 6 anderen.
Berechne also die y-Koordinate an der Stelle x = -3, -2, -1, 0, 1, 2 und 3.
Genau wie ich es oben vorgemacht habe. Die Zahlen die ich gerade aufgezählt habe einfach in die Funktion einsetzten und das ganze ausrechen.
Das, was dann rauskommt ist wie du siehst dann immer "y =", also die y-Koordinate.
Ich hoffe ich konnte das ganze verständlich erklären.
_______________________________________________
Wenn du dann insgesamt 7 Punkte eingezeichnet hast kannst du die Parabel auch zeichnen. Dann ist das Nullstellen ablesen ein leichtes. In dem Bild siehst du das aber auch schon.
Die Nullstellen sind N( -4 | 0) und N1( 1 | 0).
_______________________________________________
Falls du noch Fragen hast kannst du sie natürlich gerne stellen! :)
Liebe Grüße
TechnikSpezi
Du machst die typischen Anfänger & Flüchtigkeitsfehler, die ich auch in der Oberstufe noch ständig mache! -.-
Fangen wir mit x = -1 an.
Setzten wir ein:
y = (-1)² + 3* (-1) -4
So musst du das auch aufschreiben, nicht anders ohne Klammern.
Daher kommt nämlich genau das, was du falsch gemacht hast.
Jetzt rechnest du erst einmal (-1)², also einfach (-1) * (-1). Was ergibt - mal - noch einmal? Genau, plus!
Also kommt bei dem Teil schon einmal 1 raus.
Weiter geht es:
3 * (-1)
Hier rechnest du also + mal -. + mal - sind wie du wissen solltest dann minus. 3 * 1 sind 1, also kommt hier -3 raus.
Am Ende dann natürlich die -4 nicht vergessen.
Also fassen wir zusammen:
y = 1 - 3 - 4
y = -6
Du hast sicherlich die Vorzeichen nicht korrekt "berechnet" und irgendwo Vorzeichenfehler gemacht. Wie gesagt, solche Fehler mache ich bis heute noch -.- ;)
Merke dir immer das mit:
+ mal - = -
- mal - = +
+ mal + = +
Das musst du im Schlaf können! Und denke dran, die Klammern zu schreiben. Damit vermeidest du solche Fehler und von der Schreibweise musst du es auch so machen, sonst gibt es Punktabzug in der Klassenarbeit!
Sicherlich kommen daher auch die Fehler bei den anderen Werten.
Probiere es jetzt nochmal und achte immer ganz genau auf die Vorzeichen! :)
Liebe Grüße
TechnikSpezi
Wow, vielen lieben Dank dir, jetzt habe ich es endlich verstanden! :)
Freut mich sehr das zu hören!! :))
Bitte bitte, da mussten wir alle mal mit genau diesen Problemen durch! ;)
allgemeine Form y=f(x)= a2 * x^2 + a1*x+ao
a2>0 Parabel nach oben offen
a2<0 Parabel nach unten offen
Scheitelkoordinaten bei x= - (a1)/(2 *a2) und y= - (a1)^2/(4 *a2) + ao
Scheitelpunktforn y=f(x)= a2 *(x+b)^2 + c
b= - x und C= y
Bei dir a2=1 und a1=3 und ao= - 4 eingesetzt
x= - 3/(2*1)= - 1,5 und y= - (3)^2/(4*1) - 4= - 6,25
mit b= - x= - * (-1,5)= 1,5 und c=y= - 6,25
eingesetzt ergibt y=f(x)= 1 * (x +1,5)^2 - 6,25
Schnittpunkt mit der y-Achse ergibt x=0
y= 1 *0^2 + 3 *0 - 4= - 4
Nullstellen mit der p-q-Formel siehe Mathe-Formelbuch
x1= 1 und x2 = -
Also wichtige Stellen sind Nullstellen x1=1 x2=+ - 4
y- Durchgang bei x=0 y= - 4
Scheitelkoordinaten bei x= - 1,5 und y= - 6,25
HINWEIS: Die Formeln für die Scheitelkoordinaten ergeben sich durch die allgemeine Umformung mit der "quadratischen Ergänzung",der allgemeinen Form in die Scheitelpunktform.
Setz den Wert für x ein und rechne y damit aus. Dadurch bekommst du einen Streckenzug von 7 Punkten und kannst aus dem Graphen die Nullstellen herauslesen.
Du erhältst die Scheitelpunktform ganz einfach durch quadratisches Ergänzen:
y = x² + 3x - 4
1. Schritt: Welche binomische Formel?
Da wir den Ausdruck +3x vorfinden, verwenden wir die 1. Binomische Formel (a + b)² = a² + 2ab + b² .
2. Schritt: Vergleich der Funktion mit der ausmultiplizierten binomischen Formel:
x² entspricht a² → a = x
3x entspricht 2ab → da a = x ist, muss 3 = 2b sein. Damit muss b = 1,5 sein.
b² muss demnach 1,5² = 2,25 sein.
3. Schritt: Quadratisch Ergänzen
Schreibe nun y = x² + 3x - 4 so, dass y = x² + 3x + 2,25 - 2,25 - 4
4. Schritt: Wende die binomische Formel rückwärts an:
y = (x² + 3x + 2,25) - 2,25 - 4 = (x + 1,5)² - 6,25
Damit bist du fertig!
Wenn du bereits die Ableitung kennengelernt hast, kannst du damit ganz einfach den Scheitelpunkt des Graphen bestimmen.
y' = 2x + 3
0 = 2x + 3
x = -1,5
y(-1,5) = -6,25
Daraus ergibt sich der Scheitel bei (-1,5/-6,25) und damit die Scheitelpunktform y = (x + 1,5)² - 6,25 .
Du bist da etwas zu weit gegangen.
Die Aufgabe lautete folgendermaßen:
Zeichnen Sie den Graphen mithilfe einer Wertetabelle mit 7 Wertepaaren, lesen sie die Nullstellen ab.
Das was ich dick markiert habe sagt ja alles. Mithilfe einer Wertetabelle. Dafür brauchst du hier keine Umformung oder quadratische Ergänzung und erst Recht keine Ableitung am Ende, die er garantiert noch nicht kennen gelernt hat. Wenn man sich mit Ableitungen beschäftigt, also in NRW in der EF (10. Klasse Gymnasium / 11. Klasse Gesamtschule), dann arbeitet man mit ganzrationalen Funkitonen und dementsprechend fast nie mit quadratischen Funktionen.
Er soll die Nullstellen ja nicht einmal berechnen, sondern ablesen.
Wie in meiner Antwort zu lesen muss man hier einfach nur die 7 x-Werte einsetzten und ausrechnen. Die Punkte in ein geeignetes Koordinatensystem zeichen und daraus eine Parabel machen. Nullstellen ablesen und getan ist die Aufgabe!
Da hast du recht. Ich habe mich allen Anschein nach nur davon leiten lassen, dass er bisher nur mit der Scheitelpunktform einen Graphen zeichnen kann und ich ihm dahingehend weiterhelfen wollte. Danke für den Hinweis.
Aus dieser Form kannst du den Scheitel nicht erkennen.
Nullstelle musst du mit pq/abc berechnen: x²+3x-4=0
Y-Achsenabschnitt: x=0 setzen: y=-4
Für die Umwandlung in die Scheitelpunktform gibt es eine Formel.
Das sollte dir weiterhelfen:
Unter "lesen sie die Nullstellen ab" versteht man nicht
Nullstelle musst du mit pq/abc berechnen: x²+3x-4=0
Das ist sicher auch eine Möglichkeit, aber hier nicht gefragt!
Stimmt, ist aber meiner Perspektive nach algorithmicher "Kindergarten", deswegen vergisst man die "einfachen" Sachen ;)
Vielen, vielen Dank für die ausführliche Antwort!! :)
Ich habe jetzt mal die anderen Zahlen in die Gleichung eingegeben, zum Beispiel -1
-1² + 3*-1-4 da kommt aber -8 raus und nicht -6, wie es laut deiner Zeichnung sein sollte :( was mache ich falsch?
Bei den anderen Zahlen (-3,-2,-1 und 1,2,3) kommen auch ganz andere Zahlen raus..