Was ist die Lösung zu diesem Mathe Rätsel?
Ich würde mich sehr für Hilfe freuen. 🙇♀️

5 Antworten
Hallo,
da gibt es keine Lösung.
Nenne die Unbekannten in den Kästchen von links oben über rechts oben und links unten bis rechts unten a, b, c und d.
Dann hast Du ein Gleichungssystem von vier Gleichungen:
a+b=8
c+d=6
a+c=13
b+d=8
Aus b+d=8 folgt b=8-d.
Eingesetzt in a+b=8 ergibt das a+8-d=8, also a-d=0, daher a=d bzw. d=a.
Wenn c+d=6 und d=a, dann c+a=a+c=6.
Das steht aber im Widerspruch zur dritten Gleichung a+c=13, denn a+c kann nicht einmal 6 und einmal 13 ergeben.
Folglich: Keine Lösung.
Entweder will Dich Dein Vater für dumm verkaufen oder er hat sich verschrieben.
Herzliche Grüße,
Willy
Setze für die Kästchen die Unbekannten u, v, w, x ein. Bilde ein Lineares Gleichungssystem mit vier Unbekannten, z.B.
u + v = 8
u + w = 13
etc.
Löse das Gleichungssystem mit den bekannten Methoden.
Hallo erstmal vielen lieben Dank für die schnelle Antwort. Leider habe ich das bisher nicht gelernt, die Frage hat mir mein Vater gestellt. Ich habe es nachgeschlagen aber leider verstehe ich das alles auf Anhieb nicht ganz. Könnten Sie mir vielleicht die Lösung schreiben? Vielen lieben Dank im Voraus :)
Nein, ich gebe keine Lösungen hier auf GF, nur Hinweise zur Lösung.
Die Kästchen werden durch die Variablen a,b,c,d ersetzt und man erhält nach Gleichsetzen a+b=b+d (weil a+b=8 und b+d=8), daraus würde folgen a=d, das kann aber nicht sein.
Somit hat das Rätsel keine Lösung
Es gibt hier keine Lösung.
Nehmen wir das ganze als Gleichungssystem mit 4 Variablen:
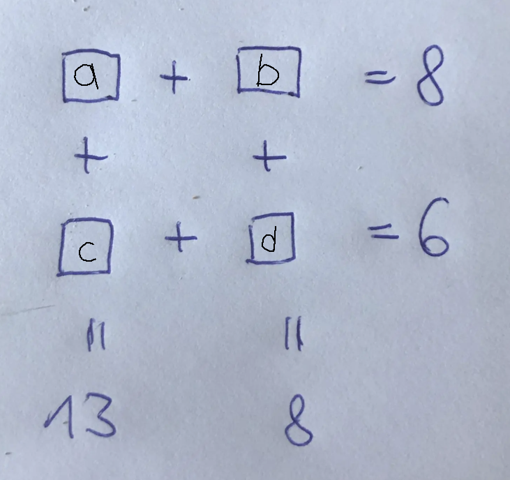
Daraus ergibt sich:
- a+b=8
- a+c=13
- b+d=8
- c+d=6
Daraus folgt:
1' -> a=8-b
2' -> a=13-c
--> 8-b=13-c
3' -> b=8-d
--> 8-(8-d)=13-c
4' -> c=6-d
--> 8-(8-d)=13-(6-d)
8-8+d=13-6+d
d=7+d |-d
0=7 -> k. Lösung
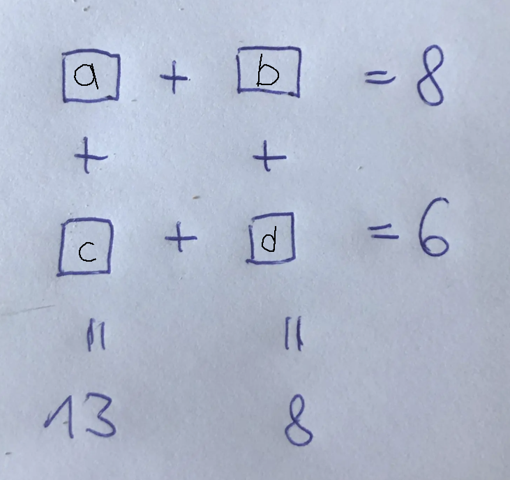
Hallo, falls immer noch Unklar: In der dritten Zeile müsste subtrahiert werden um das Rätsel zu lösen.
mfG
Hallo,
noch einfacher ist es zu erkennen, wenn die Gleichungen addiert werden.
a+b=8
c+d=6
--> a+b+c+d=14
a+c=13
b+d=8
--> a+b+c+d=21
14≠21
🤓