Warum muss eine Integralfunktion zwingend eine Nullstelle haben?
Kann mir das jemand verständlich erklären?
4 Antworten
Eine Integralfunktion ist eine Funktion F, deren Funktionsgleichung von der Form...
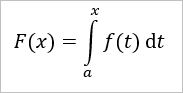
... ist. Für eine solche Funktion hat man dann eine Nullstelle bei x = a. Denn...
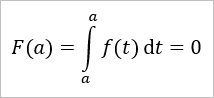
[Wenn obere und untere Integralgrenze übereinstimmen, ist das Integral gleich 0. Denn dann ist quasi der Intergrationsbereich eine Nullmenge.]
Dementsprechend hat jede Integralfunktion mindestens eine Nullstelle (nämlich die untere Integralgrenze).
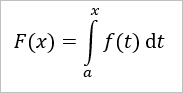
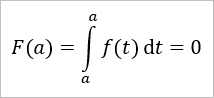
Bei einer Integralfunktion ist die untere Grenze fest und die andere die Variable (z.B. x). Setzt man für dies x den gleichen Wert wie die untere Grenze, ist das Integral logischerweise null.
Die eine Nullstelle, die eine jede Integralfunktion zumindest haben muss, liegt auf der unteren Integralgrenze. Das macht ja Sinn - eine Fläche (und somit das betreffende Integral), die von x1=a bis x2=a reicht, ergibt nun einmal 0.
Also ich beziehe mich hier auf mein 12.-Klass-Mathebuch Lambacher Schweitzer von Klett, S. 13, und einige Skriptseiten meines studierten Mathelehrers. Vielleicht ist meine Formulierung nicht ganz günstig, aber ein Integral mit der oberen und unteren Grenze a ergibt nun einmal 0.
Du hast recht, und ich nicht. Tut mir leid, hatte zwei Stiefel miteinander verwechselt.
Muss sie nicht.
Aber wenn sie welche hat, musst du von Nullstelle zu Nullstelle integrieren, sonst werden die Flächen unter der x-Achse subtrahiert.
Also uns wurde auch beigebracht, dass jede Integralfunktion mindestens eine Nullstelle hat.
Eine Integralfunktion hat nur genau dann immer gewiss mindestens eine Nullstelle, wenn es sich bei der zu integrierenden Funktion um eine Differenzfunktion zweier Funktionen (Stichwort gestrandeter Wal) handelt.
Vorausgesetzt, die Funktionen berühren sich wenigstens.
In diesem Fall wurde euch offenbar etwas falsches beigebracht.
Ich glaube, du benutzt den Begriff Integralfunktion irgendwie anders, als er in der Mathematik definiert ist. Eine Integralfunktion ist die Funktion, die sich ergibt, wenn man bei einem bestimmten Integral die obere Grenze mit der Variablen x ersetzt. Oder anders gesagt: Wenn ich ein bestimmtes Integral als Funktion seiner oberen Integrationsgrenze betrachte, erhalte ich eine Integralfunktion. Und diese Funktion hat tatsächlich immer eine Nullstelle, nämlich die untere Integrationsgrenze, wie LaraCM auch erklärt hat.
Alles klar, mein Fehler, sorry! Ich hab den Begriff der Integralfunktion mit der integrierten Funktion anstelle der zu integrierenden Funktion gleichgesetzt.
Hab ich mir fast gedacht. ;) Dafür kenn ich auch keinen guten Namen, außer vielleicht Stammfunktion.
Im Nachhinein macht's völlig Sinn, denn genauso wie die Logarithmusfunktion aus einer gegebenen Funnktion den Logarithmus bildet, bildet die Integralfunktion eben das Integral. Deutsche Sprache, schwere Sprache :P
Keine Ahnung, ich kenn deinen Lehrer ja nicht. Wenn er das so gesagt hat, ist das jedenfalls eindeutig falsch.
Halt - dein Lehrer hat recht, dank des Kommentars von PhotonX ist mir jetzt klar, worauf das Missverständnis aufbaut. Sorry!
Erstens ist das unsinnig, weil zwei verschiedene x-Stellen nicht denselben x-Wert besitzen können, zweitens kannst du weder ein Integral noch eine Fläche bilden, wenn du nur eine Integralgrenze a gegeben hast.