Warum kann eine stammfunkion ohne nullstelle keine integralfunktion sein?
Wenn bei einer integralfunktion die obere Grenze gleich der unteren Grenzen ist, liegt dort eine Nullstelle der Funktion. Denn F(a)-F(a)=0. ich verstehe die Aussage oben aber nicht ganz. Vlt kann mir die jemand erklären 😬.
4 Antworten
Hallo Antonia430,
die Funktion F selbst muss überhaupt keine Nullstelle haben. Beispielsweise ist für
(1) F'(x) = f(x) = –λ·e–λ·x
die Stammfunktion
(2) F(x) = e–λ·x.
Wenn wir jetzt eine Stelle x=a als ,,untere" Integrationsgrenze haben (die ,,obere" Grenze x=b kann auch kleiner sein, allerdings dreht die Vertauschung der Grenzen das Vorzeichen des Integrals um), hat allerdings die Funktion
(3.1) F(x) – F(a),
in unserem Beispiel
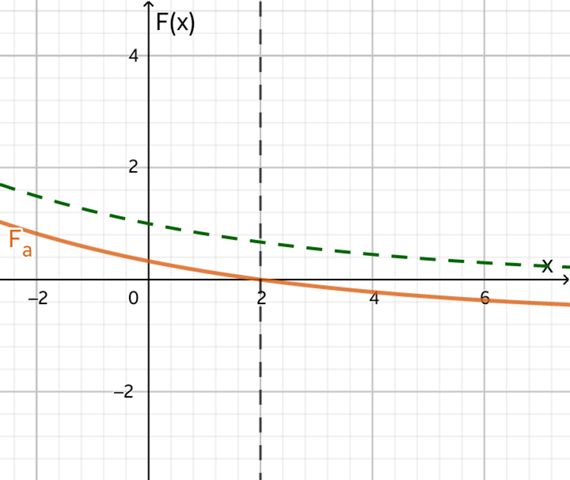
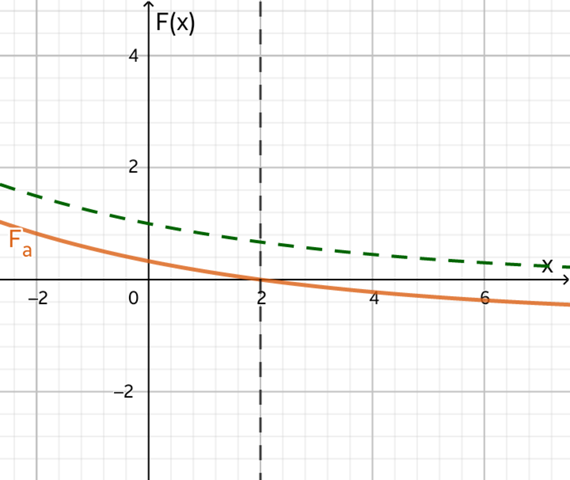
(3.2) Fa(x) = eλ·x – eλ·a,
automatisch eine Nullstelle bei x=a, denn die Subtraktion der Konstanten eλ·a verschiebt den Graphen so weit nach unten, dass Fa(a) gleich 0 ist.
Eine Funktion f ist eine Integralfunktion, wenn es reelle Zahlen a und k sowie eine integrierbare Funktion g gibt, sodass gilt:
Dann hat f immer eine Nullstelle bei x=a, denn
_____
Wenn f also eine Integralfunktion ist, hat f eine Nullstelle. Die Umkehrung dieser Aussage liefert dann, dass eine Funktion ohne Nullstelle keine Integralfunktion sein kann. f kann aber trotzdem eine Stammfunktion sein.
Die Funktion f(x)=x²+1 hat bspw. keine reellen Nullstellen, ist aber eine Stammfunktion von g(x)=2x. Es gibt jedoch keine Funktion g, für die f definitionsgemäß eine Integralfunktion wäre.
Von einer Stammfunktion für g kann man leicht auf die Integralfunktion schließen, denn man muss nur die ggf. vorhandene Konstante weglassen; man berechnet ja ein bestimmtes Integral, wodurch die Konstanten rausfallen.
Im Beispiel unten wäre also h(x)=x² die eindeutige Integralfunktion von g(x)=2x.
Weil jede Integralfunktion eine Nullstelle hat, zum Beispiel wenn der Interval von a bis a geht oder: F(a)-F(a)=0
Bin mir nicht sicher aber:
Joa, das kommt halt mit der Bedinung, dass eine Stammfunktion F(x) die Integralfunktion ist wenn F'(x)=f(x) ist.
erstmal : was soll der sinn sein von F(a)-F(a)=0............. das gibt doch keine Fläche ?
...........................................
Wenn die Stammfkt eine Parabel ist , kann sie keine NSt haben . z.B ax^2 + b
Andererseits ist bei der SFkt immer der Summand +C . Daher hat sie immer eine NSt.
Wenn f a (a) —> 0
sie kennen sich schon mit integralfunktionen aus oder?😬 oder steh ich jetzt aufm Schlauch? Eine stammfunktion ist nur eine integralfunktion wenn sie eine Nullstelle hat.. aber es gibt doch auch stammfunktionen die keine ns haben.. warum sind dass dann keine integralfunktionen?
Streich das mit dem k. Es reicht f(x)=Integral_{a;x} g(t) dt