Vollständige Induktion Summenzeichen?

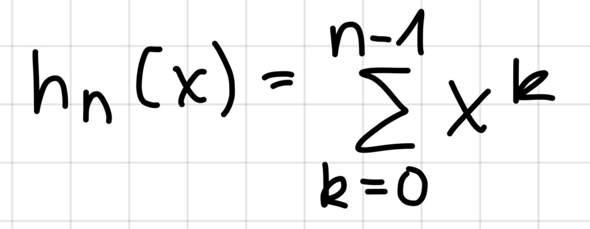
Ist meine Formel richtig so? Würde sie gerne durch Induktion beweisen, aber weiß überhaupt nicht, was ich machen soll. Kann mir bitte wer helfen?

Answer 1

[mihisu]

Ja, die Formel für h_n passt.

Zum Beweis mit vollständiger Induktion...

Die Lücke bei den rot markierten „[...]“ musst du jetzt noch füllen.

Als weiteren Hinweis, falls du noch nicht weiterkommst, gebe ich noch:

$x^{n+1}-x^n+x^{n}-1$

======Ergänzung======

Möglicher vollständiger Beweis zum Vergleich: https://i.imgur.com/vdxyl8O.png

Comments

[mihisu]

Ich habe versehentlich h₀ im Induktionsanfang stehen, wo eigentlich h₁ stehen sollte. (Ich bin aber zu faul, das in den Bildern auszubessern.)

Answer 2

[eterneladam]

... beispielsweise mit Induktion ...

OK, wenn man Induktion üben will, aber direkt ausrechnen geht auch,

Summe( k=0; n-1; x^k ) ( x-1) =

Summe( k=0; n-1; x^(k+1) ) - Summe( k=0; n-1; x^k ) =

x^n - 1

Answer 3

[Littlethought]

Es ist leicht zu zeigen, dass die Formel für n=1 richtig ist .

Annahme: Die Formel ist richtig für N. => p_N(x) = x^N - 1 = (x-1) * h_N(x)

Es ist zu zeigen, dass die Formel dann auch für N+1 richtig ist.