Umkehrbare Funktion, Begründung?

Handelt es sich hier um umkehrbare Funktionen?

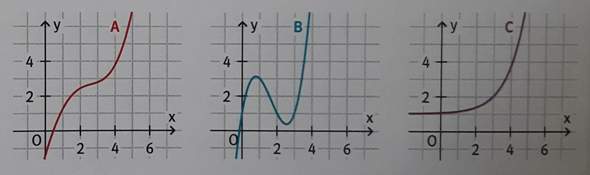
Ich bin mir nicht sicher aber ich denke A und C sind umkehrbar und B nicht umkehrbar. Aber wie kann man das begründen?

Answer 1

[HeniH]

Hi,

ich weiß ja nicht, wie bekannt die Begriffe surjektiv, injektiv und bijektiv Dir sind?

Deswegen würde ich bei der Begründung bleiben:

B ist nicht umkehrbar, weil sie nicht streng monoton wachsend ist auf R!

Deine Entscheidungen sind richtig, A und C sind umkehrbar und B nicht.

LG,

Heni

Woher ich das weiß: Studium / Ausbildung

Comments

[gilam]

Okay danke! Die Begriffe kenne ich nicht, aber wie kann man dann begründen das A und C umkehrbar sind?

[HeniH]

@gilam

Eben, in dem Falle, weil sie streng monoton steigend sind, also keine lokale Extrempunkte haben. Das reicht in dem Falle, wenn Du noch nicht die oben gennaten Begriffe kennst.

Answer 2

[Ellejolka]

wenn du die Funktion von B) an der 1. Winkelhalbierenden spiegelst, entsteht keine Funktion.

und weil f nicht injektiv ist.

Answer 3

[SevenOfNein]

Bei b gibt es zu einigen y Werten zwei x Werte. Deshalb ist sie nicht umkehrbar.

Woher ich das weiß: Hobby