Überprüfung meiner Matheaufgabe ( :?
Es geht um folgendr Aufgabe: Gegeben ist die Funktion f mit f(x) = 1/5 * x ^ 2 * (6 - x) . Der Punkt P(u|v) mit 0 < u < 6 liegt auf dem Graphen von f. Die Koordinatenachsen und die Parallelen zu den Achsen durch P bilden ein Rechteck. Bestimmen Sie u so, dass der Flächeninhalt des Rechteckes maximal ist.
Und dies ist meine Lösung dazu:
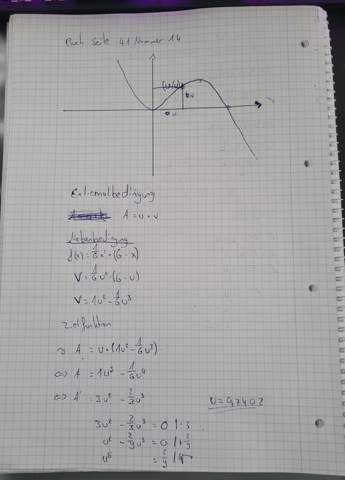
Ich habe jetzt nichr auf alle Formalia geachtet müsste aber dennoch das korrekte Ergebnis haben ( : Ich hoffe, dass mir dies jemand bestätigen kann.
1 Antwort
Hallo,
deine Rechnung ist richtig bis zur Gleichung
Danach stimmt es nicht mehr.
Man sucht Nullstellen von A' die zwischen 0 und 6 liegen. Es gilt
Die Nullstellen von A' sind 0 und 9/2 = 4,5 .
Die Null als Nullstelle muss man ausschließen.
Es bleibt also die Nullstelle 4,5 die zwischen 0 und 6 liegt.
Nun müsste man noch prüfen, ob A''(4,5) < 0 gilt (und das ist der Fall).
Gruß
Aber warum sucht man denn die Nullstellen. Es soll doch etwas maximal werden. Wenn Ich die >Nullstellen von A´ berechne dann kommt bei mir wie oben genannt das besagte u heraus.
Du hast die Gleichung
u² - (2/9)u³ = 0
Jetzt addierst du auf beiden Seiten 2/9, das ergibt aber nicht u⁵ = 2/9 ,
das ist falsch!
Wenn du auf beiden Seiten der Gleichung 2/9 addierst, erhält man
u² - (2/9)u³ + 2/9 = 2/9
und das bringt nichts.
Man kann aber u² ausklammern:
u² (1 - (2/9)u) = 0
Ein Produkt ist Null, wenn einer der Faktoren Null ist. Das bedeutet,
dass entweder u = 0 ist, oder 1 - (2/9)u = 0 .
u = 0 muss man als Lösung verwerfen wegen der Bedingung 0 < u < 6 .
Es bleibt 1 - (2/9)u = 0 <=> 1 = (2/9)u <=> u = 9/2 .
Ich konnte dir nur teilweise folgen. Also man muss die Nullstellen berechnen, weil man so üblicherweise die Extremstellen berechnet. Aber ich habe doch auch die Nustellen berechnet. Wo habe ich denn dort einen Fehler gemacht und was wäre eig. wenn das Ergebnis nicht zwischen 0 und 6 liegt.