Straßensteigungen?
Kann mir jemand bitte helfen ?
a) Auf einem Straßenschild ist die Länge s der Straße mit 7 km und die Steigung m mit 9% angegeben. Wie groß sind der Höhenunterschied h und die horizontale Entfernung ?
b) wie lang ist eine Straße die bei einer Steigung von 6% eine horizontale Entfernung a von 12 km überwindet ?
5 Antworten
Die Prozentangabe der Steigung bezieht sich auf den Höhenunterschied zur horizontalen Entfernung. In diesem Fall beträgt der Höhenunterschied (h) also 9 Prozent der horizontalen Entfernung (a). h = 0,09a
Bei diesem rechtwinkligen Steigungsdreieck ist die Straßenlänge die Hypothenuse und die horizontale Entfernung und der Höhenunterschied sind die Katheten.
s² = a² + 0,09a²
Jetzt müsstest Du allein weiterkommen.
a)
9% Steigung bedeutet, dass man 9 Höhenmeter gut macht, auf 100 Meter Entfernung. Daher auch 9/100 = 9 pro Hundert = 9%.
Da sich einige darüber aufregen, dass ich dir nicht die 100% korrekte Variante an die Hand gegeben habe, hole ich das nun nach:
Die Straße entspricht der Hypotenuse in diesem Beispiel. Diese ist 7000 lang. Auch kennen wir die Steigung von 9%, wir wissen also, dass das h nur 9% von a entsprechen darf. Daher gilt
s² = a² + h²
s² = a² + (0,09a)²
s² = a² + 0,0081a²
7000² = 1,0081a²
a² = 7000² / 1,0081
a = Wurzel(49.000.000 / 1,0081)
a = 6971,82
Da h = 0,09a sein muss, ergibt das für h:
h = 0,09a
h = 6971,82 * 0,09
h = 627,46m
b)
Diesmal ist die Hypotenuse gesucht.
a² + b² = c²
a = 12000 meter
b = 6% von 12000 meter
Als Tipp: Die Straße wird irgendwas zwischen 12000 und 12050 Metern lang sein.
Ist es doch auch, wenn es irgendwo zwischen 6950 und 7000 metern liegt, oder nicht? :D
Aber wenn du sehr viel Wert darauf legst, kann ich die 7000 auch zu 6999 abändern. ;-)
Verständnisfrage zu a) (Ich rechne auch gerade wie wild...) Und ich denke das a) nicht richtig ist. Ich kann jetzt um die Zeit aber a) auch nicht errechnen. Wenn die Straße s 7000m lang ist, heißt das nicht, dass man bei 100% 1m Höhe auf auf einem Meter Strecke zurücklegt. Schau Dir das mal bei einem Geometriedreieck an. Die Steigungsverhältnis bezieht sich meiner Meinung auf a! Um 10cm Höhe zu gewinnen bei einer Steigung von 45° bzw. 100% muss ich nämlich um die 15cm zurücklegen. Was meinst Du?
7000 Meter ist die Hypotenuse, in der Grafik als s dargestellt. Die Höhenmeter sind als h eingezeichnet. 9% von 7000 sind? 630 meter.
7000² = 630² + a²
a² = 7000² - 630²
a = ?
Ich denke also doch, dass es richtig ist. Die Gradzahl der Winkel kennen wir nicht (aus dem Text zumindest), einzig der Winkel unten rechts ist angegeben.
Wir könnten die Gradzahlen nun durch die Strecken ermitteln, aber für einen 45° Winkel müssten h und a exakt gleich lang sein (schließlich wäre der dritte Winkel dann auch 180° - 90° - 45° = 45°).
Um das ganze mal bildlich auszudrücken: Das ergäbe eine Steigung von 1m auf 1m = 100%. Also nein, du musst dich sehr irren. :D
Guten Morgen... Ich habe gerechnet und 9% von c = 7000m sind 494m Höhengewinn. Das muss mit Winkelfunktion gerechnet werden. Wie Du richtig schreibst sind 45° 100%! Ein Unimog der eine Steigung von 45° fährt legt einem Meter Strecke 1m an Höhe zu. a²+ b² = c² c² = Wurzel aus 2 = 1,41m! Wie DU siest irre ich mich nicht! ^^
"Wenn die Straße also 7km lang ist, was 7000 Metern entspricht, dann verhält sich
x zu 7000 Metern, wie 9 zu 100 Metern"
Der Unterschied ist zwar nicht gravierend, aber der Ansatz ist falsch. Mach dir eine Skizze dazu...
Aber gut, rechnen wir deinen Weg:
h = 0,09a
s² = a² + (0,09a)²
s² = a² + 81 / 10000 a²
s² = 1,0081a²
s = 1,0081a
a = 7000 / 1,0081
a= 6943,76 m
Da h 0,09a sind, entspricht das einem h von ca 624,94 m.
Und nun kommt die alles entscheidene Frage: Denkst du ernsthaft, dass jemand, der solch simplen geometrischen Figuren berechnen soll, in der Lage wäre, eine entsprechende Gleichung aufzustellen?
Für mich sieht das nach Klasse 7 Mathe aus, nicht nach Oberstufen Mathematik.
@@oetscha Sogar noch falsch gerechnet zu so später Stunde:
s² = 1,0081a²
a² = s² / 1,0081
a² = Wurzel(49.000.000 / 1,0081)
a = 6971,82
Damit ergibt sich ein h von 627,464 m
Gute Antwort kann. Ich denke wir alle haben odrr hatten das Problem, was 9% heißt
Mir ist durchaus bewusst, dass es eigentlich nicht zu 100% stimmt, allerdings bleibt das Argument bestehen, dass es Unterstufen-Mathematik ist.
Jemand der bereits Hilfe braucht, weil er die Aufgabenstellung trotz Skizze nicht verstanden hat, wird kaum in der Lage sein, die Gleichung entsprechend umzuwandeln.
Ich bezweifel auch, dass es vom Autor ursprünglich so gedacht war (wie gesagt, Unterstufenmathematik), daher hatte ich diesen Rechenansatz gewählt.
Nein, eigentlich ist ziemlich offensichtlich was 9% heißt, die Skizze war ja mitgeliefert. Meine Antwort basierte nur darauf, dass ich bezweifel, dass sie wirklich rückwärts rechnen sollen, mit 2 Unbekannten, die nur im Verhältnis zu einander stehen...
Das schlimme ist, dass er durch seine Gleichungsrechnung zu einem Ergebnis kommt, dass in der Probe mit dem Pythagoras aufgeht. Weil er das richtige Verhältnis der Länge aus der falschen Höhe zieht.
Deshalb finde ich den Rechenweg mit den sin für die Höhe und cos für die horizontale Strecke sicherer.
GuteAntwort2021 Die Annahme müsste heißen "h zu horizontales Strecke a, verhält sich wie 9m zu 100m"
Vorrausgesetzt man rechnet mit dem richtigen Winkel und das haben wir nicht.
Die Annahme 45°/100*9=4,05° ist Mist²... warum, muss ich mir nochmal anschauen... ^^
Wie kommst du auch auf die Idee, es könnten 45° sein? 45° Steigung wären eine 100% Steigung.
Denn dann würden beide verbliebenen Winkel 45° entsprechen, also auf jeden horizontalen Meter kämen ein Höhenmeter hinzu.
Wenn man schon klugscheißen möchte, dann doch auch bitte wissen wovon man spricht!
"Mir ist durchaus bewusst, dass es eigentlich nicht zu 100% stimmt, allerdings bleibt das Argument bestehen, dass es Unterstufen-Mathematik ist."
Sorry, aber es ist - auch in diesem Fall - völlig irrelevant, ob das nun Unter-, Ober- oder Mittelstufenmathematik ist. Wenn diese Aufgabe einem Schüler von einem Lehrer "zugemutet" wird, ist wohl anzunehmen, dass dem Schüler die dahinter stehende Theorie bereits vermittelt wurde und dass der Lehrer dem Schüler zutraut, die Aufgabe zu lösen. Wenn auch vielleicht nicht auf Anhieb - Nachdenken ist mitunter ein anstrengendes Geschäft...
Und ein falscher mathematischer Weg ist und bleibt ein falscher Weg und führt zu einem falschen Ergebnis - egal in welcher Schulstufe.
Warum musst Du so beleidigend sein?
Mir ist klar, dass 45° 100% sind. Der Irtum war, das man das nicht einfach mit einem 3 Satz umrechnen kann und die 4,05° demzufolge nicht stimmen.
Wieso beleidigen? Du kritisierst meine Antwort, schön und gut, war ja zu Recht, warum darf ich das gleiche nicht mit deiner falschen Behauptung machen.
Und wenn man etwas als falsch kritisiert, aber dann selbst nicht richtig aufstellt, dann verdient dies das Prädikat "klugscheißen". Das ist nicht beleidigend, einfach nur eine treffende Beschreibung der Szene. :P
Nein Sorry... Der Ton macht die Musik. Ich habe nur an deiner Lösung mitgewirkt... Denn von der Sache her, ist dein Rechenweg genau so richtig wie der Ansatz mit der Winkelfunktion! Da sollte auch das gleiche Ergebnis rauskommen! Es ist eigentlich armseelig, dass wir bei einer 7 Klasse Aufgabe immernoch am rechnen sind. ^^
Du kennst aber nur einen Winkel, du hast keinerlei Verhältnisfunktion von der Länge der Strecke, noch dem dazu gehörigen Winkel.
Ob man den Winkel durch die Prozent ableiten kann, weiß ich nicht. Bleiben ja nur noch 90° für die anderen beiden Winkel zusammen. Ob man die 9% nun so ins Verhältnis setzen kann?! Ich weiß es nicht.
Das war ja meine Überraschung. Ich habe gestern deine Aufabe (versucht) nachvollziehen, und habe verschieden Möglichkeiten gerechnet und habe vieeele Ergebnisse rausgebracht. Aber keins hat sich mit der Winkelaufgabe von mir gedeckt. Das liegt daran, dass die ebenfalls falsch gerechnet ist. Denn sie basiert auf die Annahme, das man von 45° = 100% 4,05°=9% augegangen ist. Das funktioniert aber so nicht. Der richtige Winkel muss ebenfalls mit Winkelfunktion gerechnet werden. Dazu kannst Du ein Dreieckmodell mit 100mm (a) und 9mm (h) verwenden. Der korrekte lautet dan 5,143° https://grad-prozent.de/ Kannst Du hier ausprobieren. 4,05° sind nämlich nur 7%... ^^ Da muss man erst mal drauf kommen. Lustig was?
Bei Winkelfunktion habe ich 2 Werte. Den Winkel und die Hypertonuse von 7000m. Die weitere Rechnung stimmt vom Weg. Nur der Winkel ist falsch. Und zwar in der Skizze und in der Rechnung. Somit stimmt da im Endeffekt gar nichts. Die Skizze, die Berechnung und die Probe... Alles Mist... Kannst Du ja schauen.
Da wir die Seiten alle kennen, können wir es auch einfach ins Verhältnis setzen:
alpha = sin^-1(627,464/7000)
alpha ~ 5,143°
Wenn ich das ins Verhältnis zu 90° setze, sind das 5,71444%. Im Verhältnis von 45° entsprechend das Doppelte.
Natürlich wissen wir, dass sin(winkel) zur gegenüberliegenden Seite immer im Verhältnis steht. Um das anzuwenden braucht man aber eben mindestens 2 Winkel mit einer dazu gehörigen Seite, oder zwei Seiten mit einem dazu gehörigen Winkel.
Das war in dem Beispiel nicht gegeben. Wir hatten lediglich die 9% Steigung. Wenn wir a gekannt hätten, hätten wir daraus auch h ermitteln können. Dann hätten wir den rechten Winkel gehabt und hätten daraus die Hypotenuse ableiten können. In der zweiten Aufgabe funktioniert der Weg also. In der ersten so aber nicht.
Nein, wir haben s=7km. Das ist die Hypotenuse. Das ist der längste Schenkel vom Dreieck und liegt dem rechten Winkel gegenüber. Suchen tun wir Ankathete (a) horizontale Strecke und Gegenkathete (h) Höhe.
Das ist das was ich denke, wo Du ins schlingern gerätst. Deshalb schwangst Du mit den 7000 in deinen Formel. Mal ist es a und mal s... ^^
Damit hast DU deine Probe bestanden... Ich werde meine Aufgabe auch noch mit dem neuen Winkel rechen. Und deine Winkelberechnung das wäre der erste Schritt bei mir gewesen nur hätte ich mit 9/100 gerechnet.
Suchen tun wir Ankathete (a) horizontale Strecke und Gegenkathete (h) Höhe.
Hä? Das ist mir durchaus bewusst? Worauf spielt diese Aussage an? Auf das ins Verhältnis setzen von 90°? Ein Dreieck hat 180°, wir haben einen rechten Winkel, fallen also 90° weg, bleiben noch? Genau, 90° in der Summe für die anderen beiden Winkel. Nicht 45°!
Daher finde ich deinen Ansatz so merkwürdig. Du setzt beide Winkel gleich, das kann aber logischerweise nicht funktionieren, da dann die Steigung 100% ist. Und für den Winkel 45° vorauszusetzen und dann 9% darauf anzuwenden, ist ein komisches Prinzip. Was passieren mit den restlichen 91%? Gehören die dann plötzlich zum anderen Winkel?
Die Summe der Winkel im Dreieck ist bei der Aufgabe wurst. Du brauchst nichts ins Verhältnis setzen. Wie Du auch schon beschrieben hast. 100m horizontale Strecke und 9m Höhengewinn ergibt eine Steigung von 9%. Jetzt willst Du den Winkel wissen: alpha = tan-1 9/100 und fertig... ^^ Und kein Dreisatz... Wie ich das gerechnet habe... ^^
Und kein Dreisatz... Wie ich das gerechnet habe... ^^
Genau das meinte ich, funktioniert nicht. Insbesondere mit 45°.
Schreibe ich ja schon die ganze Zeit... ^^ das funktioniert auch mit keinem anderen Winkel. 100% sind nunmal 45° das bleibt. Das Verhälnis Winkel zur Steigung ändert sich aber nicht linear.
100% sind nunmal 45° das bleibt.
Und genau das ergibt keinen Sinn für mich. Wieso sind 45° 100% für dich? Woher weißt du, dass der eine Winkel nicht 70° und der andere Winkel 20° ist zum Beispiel? Oder 80°|10° oder 30°|60°? Oder die unendlich vielen anderen Kombinationsmöglichkeiten?
Die 45° ins Verhältnis von 100% zu setzen ergibt absolut 0 Sinn. Eher Verständnis hätte ich für einen Rechenansatz gehabt, der die verbleibenden 90° für beide Winkel irgendwie in Relation setzt mit den 9%.
So nach dem Motto: 90 * 0,09 = 8,1° verbleiben für den Winkel [sh] also 81,9°.
Das funktioniert natürlich auch nicht, aber das wäre zumindest gedanklich noch nachvollziehbar. Die 45° hingegen kein Stück meiner Meinung nach.
Eine Steigung von 100% hat 45° Das war immer so und wird immer so sein. Das liegt schlicht am Steigungsverhältnis. Das ist wie ein Geodreieck. Wenn Du eine horizontale Strecke von 1m fährst bei einer 45° Steigung dann machst Du einen Meter gut. Das sind 100%! Es gibt Fahrzeuge die Schaffen noch mehr. Ein Unimog schafft auch 110% Das sind dann 47,72° https://grad-prozent.de/
Ja natürlich, das bedeutet aber auch, dass der andere Winkel 45° ist. Denn nur dadurch ist die Steigung 100%, da für jeden meter auf a, 1 meter auf h dazu kommen muss! Wenn du den einen Winkel verkleinerst, musst du den anderen entsprechend vergrößern, da der rechte Winkel gegenüber der Hypotenuse fix ist.
Wenn du also 45°*0,09 rechnest für Winkel alpha, dann musst du bei Winkel beta 45°*1,91 rechnen, bzw. 45°+(45-(45*0,09)).
Daher wäre die Überlegung für mich deutlich logischer, die verbleibenden 90° für beide Winkel in Relation zu einander zu setzen.
Aber da beides nicht funktioniert: Jacke wie Hose.
Das funktioniert ja auch... Aber eben nur mit tan... ^^ Passt Doch jetzt alles ich korrigier gerade mein Blatt und setze es ein. Die Ergebnisse sind deckungsgleich. Alles prima! Sieht etwas wild aus... Was solls, kannst es DIr ja nochmal anschauen...
...hat letztlich doch Spaß gemacht. Und ich habe mal wieder meine alten Zellen entrostet... ^^ Schönen Abend noch.
Mein Lösungsvorschlag...
Ich habe erstmal eine Skizze mit dem Geodreieck angefertigt.
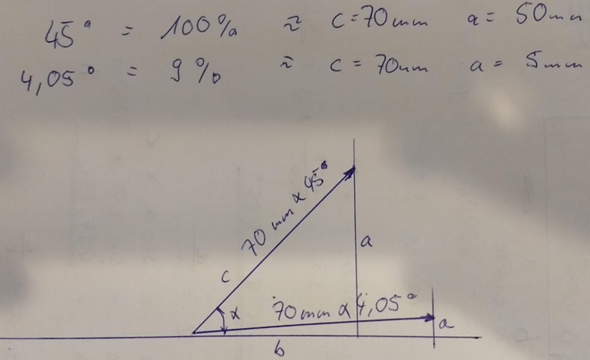
45° Steigwinkel sind 100%. Dann sind 4,05° 9% ---> Diese Annahme ist falsch. Der korrekte Winkel muss mit Winkelfunktion gerechnet werden. ---> 5,143°
alpha = tan^-1(a/b)
alpha = tan^-1(9/100)
alpha ~ 5,143°
Wenn ich eine Linie mit 70mm mit 45° Steigung messe komme ich auf 50mm Höhengewinn. Bei 5° sind es ungefähr 6mm. Auf 7000m würde das ungefähr 600m betragen.
Nun zur genauen Rechnung:
Bei Aufgabe b) ist nicht c gegeben sondern b. Sonst ist die Aufgabe im Prinzip gleich.
Genau! So denke ich auch mit sinus und cosinus. Nur bei mir kommt ne negative Zahl raus, wenn ich Sin 4,05 eingebe, nämlich -0,788. Woran liegt das?
Benutze diesen taschenrechner
9/100*360=32,4grad
Sin 32,4= h/7
H=5,83
A quadrat= 49-5,83=43,17
A=6,57
Probe mit cosinus hab ich versucht, kommt aber was anderes raus. Und statt oben 360 nur 90 Grad nehmen, kommt auch zu merkwürdigen Ergebnissen.
"kommt auch zu merkwürdigen Ergebnissen."
...was nicht verwundert, da der Ansatz völlig falsch ist.
Der Fehler ist, dass 100% Steigung 45° beträgt und keine 360°
Mercedes wirbt damit, dass eine G-Klasse das kann... Man sollte ihr auch eine Chance lassen... ^^
Mit 45 hatte ichs auch gerechnet, da kam auch Müll raus. Aber naja. Teilweise negative Zahlen durch die sinusfunktion
Danke! Ich hab so an mir gezweifelt, nun kann ich wieder schlafen.
Steigung = Höhengewinn / Horitzontalstrecke
In deinem Fall also
Steigung = h / a
Damit kannst Du alles ausrechnen.
Und Bedenke: % ist die Kurzschreibweise von 1/100
Ah Aufgabe 2, sorry. Kommentar editiert