Primzahlen?
Es geht um die erste Ziffer vorne der Primzahlen in geordneter Folge.
Folgende Regeln:
Ich bin auf einem Plattenweg am Hundehaufen und beginne mit der ersten Primzahl, der 2.
Immer wenn die erste Ziffer vorne 1,2,3 oder 4 ist, gehe ich einen Schritt nach vorne. Ich darf nicht auf die Ritzen treten, sonst bin ich tot.
Bei 5,6,7,8 oder 9 vorne gehe ich eine Platte zurück.
Wenn ich rückwärts wieder hinter dem Hundehaufen bin, dann bin ich gerettet.
Also ich laufe los:
Primzahl-> Gehwegplatten-Nr.
2 -> 1
3 -> 2
5 <- 1
7 <- 0
Jetzt bin ich wieder am Haufen. Ich bin aber erst gerettet, wenn ich dahinter bin.
11->1
13->2
...
97<-1
101->2
Eigentlich müsste ich es schaffen, aber ich komme niemals wieder hinter den Hundehaufen, immer nur in die Nähe. Ich vermute mal, ich schaffe das nie, obwohl es mehr Ziffern sind, bei denen ich rückwärts laufen muss.
Ich behaupte mal, dass das auch in der Unendlichkeit nie passieren wird.
Was genau ist nun deine Frage?
Die Frage sollte sein, ob meine Behauptung stimmt.
2 Antworten
Wenn ich es richtig verstanden habe, d.h. für jede Primzahl:
match prim_ziffer {
'1' | '2' | '3' | '4' => position += 1,
'5' | '6' | '7' | '8' | '9' => position -= 1,
};
Das stimmt mit den von dir gegebenen Nummern überein. Dann bist du bei der Primzahl 991 wieder bei -1 (hinter deinem Haufen)
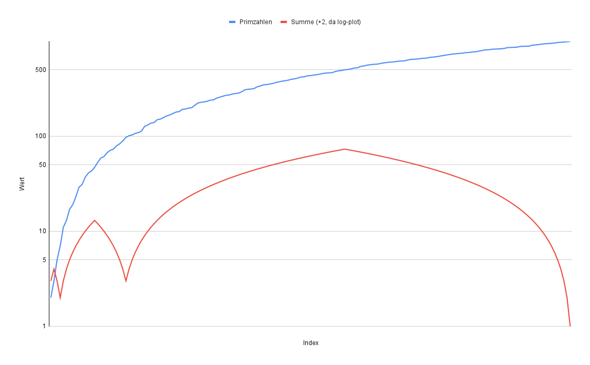
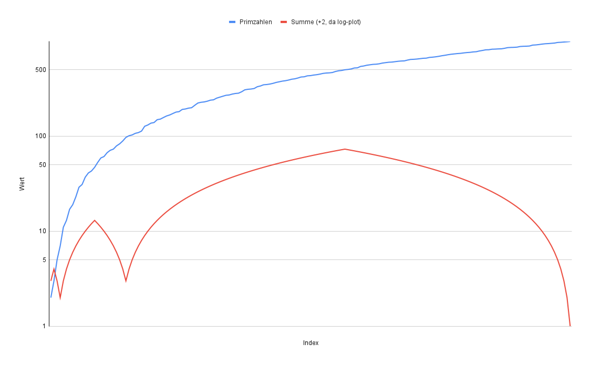
Mein Code ist folgender:
fn main() {
const UPPER_BOUND: usize = 1000;
let mut position = 0isize;
primal::Primes::all().take(UPPER_BOUND).for_each(|prime| {
let erste_ziffer = prime.to_string().chars().next().unwrap();
match erste_ziffer {
'1' | '2' | '3' | '4' => position += 1,
'5' | '6' | '7' | '8' | '9' => position -= 1,
_ => core::panic!(), // es können nur die oberen ziffern vorkommen
};
println!("{prime} {erste_ziffer} {position}");
});
}
Ich bin mir ziemlich sicher, dass dieser (bis zum 64bit unsigned integer Limit) korrekt ist. Es gibt keine negative Position vor 991, aber auch bei 99 Millionen landet man wieder hinterm Haufen. Ich kenne mich aber nicht genug mit dem Thema aus, beweise dafür zu liefern, dass dies immer wieder passiert.
Hmmm. Ich habe mir mal alle Ganzzahlen angeguckt und da gibt es eigentlich das gleiche Muster. Da kommen wir unter deinen Regeln (zumindest bis 90 Millionen) auch immer wieder ein bisschen ins Negative. Ich denke, dafür könnte man einen Beweis finden.
Wir könnten annehmen, die Kondition "Primzahl" eliminiert zufällig Einträge aus den Ganzzahlen und hat keinen Einfluss auf die Wahrscheinlichkeit jede mögliche erste Ziffer zu sehen. Das würde (soweit) hinkommen.
Die Idee habe ich erstmal wieder verworfen, denn die Dichte der Primzahlen ist ja im Bereich von z.B. 1000 bis 5000 höher als die zwischen 5000 und 10000, beim zehnfachen dessen ebenso usw. Das müsste man ja noch mit diesem Benfordschen Gesetzt abgleichen.
Aber damit lag ich vielleicht falsch, denn das Intervall von 5000 und 10000 hat ja auch wieder eine höhere Primzahldichte als zwischen 10000 bis 50000. Das irritiert mich jetzt zwar, aber doch, ich denke, Du hast damit recht. Das wäre dann ein "Beweis mit Bauchgefühl" gegen meine ursprüngliche Vermutung.
Es wird also auch mit den Primzahlen auf ewig immer kleine Ausreißer ins Negative geben, wenn auch immer seltener.
Wenn man der Folge der Primzahlen eine gewisse Zufälligkeit zugesteht, dann kann man aus dem Benfordschen Gesetz die Vermutung ableiten, dass es eher nicht zurück hinter den Hundehaufen gehen wird. Denn der Anteil der Primzahlen, die mit 1, 2, 3 oder 4 beginnen, beträgt dann um die 70%. Das ist selbstverständlich kein Beweis, und JanaL161will in seiner Antwort das Gegenteil gezeigt haben. Bliebe immer noch die Frage offen, ob du immer wieder mal hinter den Hundehaufen zurückkehrst oder irgendwann dauerhaft davor bleiben wirst.
Das zu Fuß zu machen, war von mir etwas schwerfällig. Ich habe mir eine Liste besorgt und gezählt. Sowohl Du als auch JanaL161 mit der faktischen Widerlegung meiner Vermutung haben recht.
Es gibt noch vor der Primzahl 997 einen kurzen Moment hinter dem Haufen. Geht schon wieder recht knapp zu, fast schon so, dass ich an eine Gesetzmäßigkeit glaube. Scheint aber das einzige mal zu sein.
Allerdings wird es dann eindeutiger, dass es nicht mehr zurück geht.
Zwischen 10000 und 50000 gibt es 3985 Primzahlen, während es zwischen 50000 und 100000 nur noch 2843 gibt. Damit bin ich über 1000 Platten weiter gelaufen und es geht nun lange Zeit weiter vorwärts.
Das Benfordsche Gesetzt kannte ich nicht. Es bietet einen Teil der Erklärung. Zum Anderen müsste man verrechnen, wieviel mal größer die Primzahldichte zwischen 1*10^n und 5*10^n ist, als zwischen 5*10^n und 10*10^n. Da gleicht sich wohl einiges aus, denn die Primzahlen sind ja zwischen großen Zahlen seltener. Aber wie sich das bei sehr großen Zahlen verhält, kriege ich halt nicht raus.
Ich bin jetzt mal nach Liste gegangen und glaube sogar schon bei 941, wenn ich mich nicht verzählt habe.
Aber das geht ja dennoch so krass knapp zu, dass ich das kaum für einen Zufall halte.
Allerdings hat auch eterneladam damit recht, dass es tendenziell eher nach vorne geht. Die von Dir gezeigte Widerlegung ist vielleicht eine einmalige Ausnahme. Eine Frage wäre auch, warum es bei der schon recht großen Anzahl zu so einer Ausnahme kommen kann.
Womit hast Du das Diagramm erstellt und was ist das für ein Code?