pH-abhängiges Löslichkeitsgleichgewicht berechnen?
Hallo zusammen, diese Aufgabe wird gestellt. Mein Ansatz wäre hier Ks, gesamt und Kl zu verrechnen und damit eine Gesamtdissoziationskonstante aufzustellen. Dabei verstehe ich aber nicht ganz, wie man die 5g an Bodensatz (in Konzentration umgerechnet) da mit rein bringt, da diese ja auch die Konzentration an S 2- in der Lösung beeinflussen und ich dann nicht einfach diese aus der Säurekonstante nehmen kann. Vielen Dank für jede Hilfe.

1 Antwort
Du willst 5 g ⇒ n=m/M=0.051 mol ZnS in 100 ml einer 0.1 mol/l H₂S-Lösung auflösen und fragst nach dem dazu notwendigen pH. Wenn sich das Zeug vollständig aufgelöst hat, dann beträgt c(Zn²⁺)=n/V=0.51 mol/l, und die Gesamtschwefelkonzentration ist dann c₀=(0.01+0.051)/100=0.61 mol/l. Diese Schwefelkonzentration verteilt sich pH-abhängig auf H₂S, HS¯ und S²¯. Allerdings werden wir mit dieser Zahl in eine Komplikation rennen, siehe weiter unten.
Gleichzeitig darf aber auch das Löslichkeitsprodukt Kₛₚ=c(Zn²⁺)⋅c(S²¯) nicht überschritten werden; daraus erhält man leicht, daß c(S²¯)<Kₛₚ/c(Zn²⁺) bzw. eine maximale S²¯-Konzentration von 4.9⋅10¯²² mol/l, also ungefähr ein Sulfid-Ion in der ganzen Flüssigkeit. Auf den ersten Blick sieht das unsinnig aus, aber wenn man mit Aktivitäten statt Konzentrationen rechnet, fällt dieses Paradoxon weg, und die Rechnung ist OK.
Jetzt müssen wir vom Gesamtschwefel c₀ auf den Anteil des Sulfids im Gleichgewicht kommen. Dazu ziehen wir die Säuredissoziation des H₂S heran. Da wir uns nur für Sulfid interessieren, schreiben wir die Dissoziation von H₂S so auf, daß wir beide Schritte zusammenfassen:
H₂S + 2 H₂O ⟶ S²¯ + 2 H₃O⁺ K = K₁⋅K₂ = c(S²¯)⋅c²(H₃O⁺)/c(H₂S) = 10¯²¹ mol²/l²
Im Massenwirkungsgesetz stehen immer Gleichgewichts-Konzentrationen. Wir brauchen auf jeden Fall einen stark sauren pH-Wert, also wird fast aller Schwefel als H₂S vorliegen, daher könnte man glauben, daß man einfach c(H₂S)=c₀ setzen soll. Das mißfällt mir aber, weil sich H₂S ja nur zu 0.1 mol/l in Wasser löst, wenn man nicht unter Druck arbeitet. Daher wird real das meiste H₂S ausgasen, und es bleiben nur 0.1 mol/l in der Lösung zurück.
Hier stellt sich wieder einmal die Frage, wie schlau derjenige war, der die Aufgabe gestellt hat. War er schlau, dann rechnet er mit c(H₂S)=0.1 mol/l, war er weniger hell, dann mit c(H₂S)=c₀=0.61 mol/l. Das ist aber eine psychologische, keine chemische Frage, und daher kann ich sie nicht beantworten; ich rechne einfach mit c(H₂S)=0.1 mol/l weiter. Ich habe allerdings den Verdacht, daß die Aufgabenstellung anders gemeint war; für die Lösung, wie ich sie ausrechne, ist es nämlich bedeutungslos, of man 100 H₂S-Lösung oder 100 ml Wasser einsetzt; mit Wasser gast weniger H₂S aus weil sich ein Teil im Wasser lösen kann, aber im Endeffekt kriegt man immer 0.1 mol/l als H₂S-Konzentration, weil sich einfach nicht mehr löst.
Nach diesem kurzen Exkurs können wir schnell zum Ende kommen. Die maximal erlaubte Sulfidkonzentration kennen wir bereits, und daher können wir einfach nach c(H₃O⁺) auflösen:

Also beträgt der notwendige pH ungefähr −lg(0.45)=0.34.
Eine andere Frage ist es, wieviel HCl man dazu ins Becherglas schütten muß. Dazu teilen wir das in zwei Schritte auf: Als erstes muß der Lösevorgang ablaufen
ZnS + 2 H₃O⁺ ⟶ Zn²⁺ + H₂S + 2 H₂O
und das verbraucht die doppelte Stoffmenge des ZnS, also 2⋅0.051=0.103 mol. Dann müssen aber noch 0.045 mol HCl dazukommen, um den pH auf die notwendigen 0.34 abzusenken, also brauchen wir insgesamt 0.148 mol HCl, das entspricht ungefähr 13 ml konzentrierter (12 mol/l) Salzsäure.
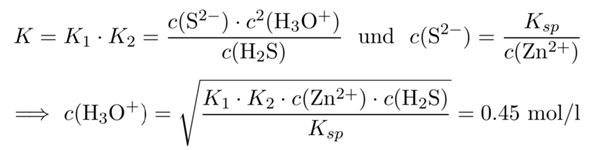
Muss dir hier einfach mal ganz herzlich Danke sagen. Durch deine Antworten sind nicht nur die Rechenschritte immer sehr gut nachvollziehbar, sondern auch die Abläufe, die hinter den ganzen Zahlen und Konstanten stehen. Das hilft einfach ungemein weiter. Also vielen vielen Dank!!
Wie kommst Du eigentlich auf diese ganzen Rechenbeispiele? Studierst Du Chemie oder irgendetwas damit Verwandtes?
Ja, im ersten Semester. Diese Fragen werden so in der Abschlussklausur gefragt. Nur sind mir die Herleitungen der Tutoren nicht immer ganz klar, weshalb ich dann gelegentlich hier nachfrage.
Kein Problem, ich rechne so etwas gerne. Sei aber gewarnt: Ich vernudle mich zwar selten beim Rechengang, aber beim Einsetzen von Zahlen mach ich dann doch öfter mal Fehler. Hauptsächlich deshalb, weil ich zu stolz bin, Papier anzupatzen, und alles auf der Tastatur kleinprügle, wobei ich zwischen Antwortschreiben im Browser, Ausrechnen mit bc und Formeln setzen mit LaTeX hin- und herwechsle. Dabei passieren gelegentlich Blödheiten.
Rechne also penibel nach und stelle eine Rückfrage, wenn es nicht paßt.
Da Du mir einen Stern geschenkt hast, frage ich mal nach: Welche Lösung wollte der Prüfer denn haben? Die mit 0.1 mol/l H₂S oder die mit 0.61 mol/l?
Die Musterlösung kommt hier auch auf den von Dir errechneten pH von 0,34, also wurde mit 0,1 mol/l H2S gerechnet.
Ich glaube - bin mir hier aber auch absolut nicht sicher - dass der Hinweis dazu ein bisschen in der Aufgabe durch die bereits anfänglich mit 0,1 mol/l „gesättigte H2S-Lösung“ gegeben war. Da wir ja die vollständige Lösung ohne weitere Fällung erwarten, ist das eventuell entsprechend zu deuten. Das wäre zumindest meine Interpretation dahinter…
Spaßhalber habe ich Google Gemini gefragt:
Erstaunlicherweise konnte Gemini die benötigten Stoffkonstanten (K₁, K₂ und Kₛₚ) recherchieren (und fand dabei leicht andere Werte als Deine, aber das ist OK). Mit der Schwefelbilanz hat er sich gar nicht erst abgegeben sondern aus meiner Sicht völlig korrekt c(H₂S)=0.1 mol/l gesetzt. Dann hat er die ganze Rechnung richtig durchgeführt, bis es ans numerische Auswerten ging:
Dabei sind die Zahlenwerte K₁=10¯⁷, K₂=1.3⋅10¯¹³, c(H₂S)=0.1 und das zuvor berechnete c(S²¯)=Kₛₚ/c(Zn²⁺), aber gerechnet mit Kₛₚ=2.5⋅10⁻²² mol²/l². Wenn man das alles einsetzt, dann kommt aber 1.63 mol/l heraus, die 10¯⁴ hat er einfach daherhalluziniert und dann knallhart einen pH von 3.79 ausgerechnet. ☺