Chemie Uni?
40 ml einer 0,1 molaren Alanin-Lösung soll mit Natronlauge versetzt werden. Wie viel Milliliter Natronlauge der Konzentration 0,1 mol/L müssen Sie dazugeben, damit Sie eine Pufferlösung mit pH = 9,9 erhalten?
Kann mir jemand mit dieser Aufgabe helfen. Sitze seit 3 stunden schon dran und habe weder einen Ansatz noch eine Idee. bitte eine Rechnung beifügen :)
2 Antworten
Die pKₐ-Werte von Alanin betragen 2.34 und 9.87; da Alanin das Zwitterion ist, also die bereits einfach deprotonierte Stufe, heißt das, daß eigentlich nur pK₂ von Relevanz ist, weil Alanin funktional einbasig ist.
Wir können uns jetzt ausrechnen, was passiert, wenn man zu einer 0.1 mol/l Alanin-Lösung 0.1 mol/l NaOH zugießt: Das Zwitterion wird deprotoniert zum Anion. Der pH steigt anfangs sehr rasch an, bleibt aber dann aber näherungsweise konstant:
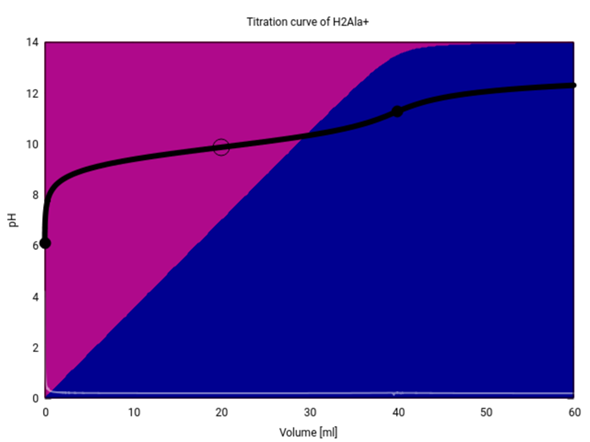
- Der Pufferbereich liegt rund um 20 ml Zugabe, wenn Zwitterion (violett) und Anion (blau) in ähnlichen Mengen vorliegen. pH=9.9 wird bei Zugabe von 20.7 ml NaOH erreicht.
- Bei 40 ml Zugabe liegt formal eine Lösung von Natriumalanat vor, also der anionischen Spezies. Es gibt auch einen ganz kleinen pH-Sprung
Hätten wir uns die 20.7 ml bis zu pH=9.9 auch zu Fuß ausrechnen können? Ja, klar, mit der Henderson–Hasselbalch-Gleichung, die den Pufferbereich gut beschreibt.
pH = pK₂ + lg (Anion/Zwitterion) = pK₂ + lg (V/(40−V))
und das kannst Du entsprechend auflösen. Oder DU kannst grob abschätzen, daß der pH=9.9 ziemlich genau dem pK₂ entspricht, und daß Du daher ziemlich genau gleich viel Zwitterion wie Anion brauchen wirst, also ca. 20 ml NaOH-Zugabe, oder 2 mmol NaOH zu den 4 mmol Aminosäure, damit die Hälfte deprotoniert wird.
In epischer Länge:
pH = pK₂ + lg (V/(40−V))
pH − pK₂ = lg(V/(40−V))
10ᵖᴴ¯ᵖᴷ² = 10⁹·⁹¯⁹·⁸⁷ = 10⁰·⁰³ = 1.07 = V/(40−V)
1.07⋅(40−V) = 42.9 − 1.07 V = V
V = 42.9 / 2.07 = 20.7 ml
Hast du mittlerweile einen Lösungsweg für die Aufgabe gefunden ? Ich komme nämlich auch nicht auf 20 ml . Wäre wichtig, weil bald die Uni Chemie Klausur ansteht. Taschenrechner sind ja nicht zugelassen
Meinst Du mich?
Schnelle Antwort: Die Henderson–Hasselbalch-Gleichung arbeitet mit Konzentrationen. Aber weil beide Stoffe (das Paar aus konjugierter Säure/Base) in derselben Lösung leben, kann man auch die Stoffmenge verwenden (das Volumen kürzt sich raus). In diesem Fall sind die Stoffmengen aber proportional zum Verbrauch an Maßlösung, also wieder einem Volumen. Das ist verwirrend.
Der Äquivalenzpunkt liegt bei Vₑ=40 ml, also enthalten 40 ml Maßlösung genau gleich viel Stoffmenge wie die Probenlösung. Wenn Du z.B. nur 10 ml Maßlösung zugibst, dan liegt ¼ der Stoffmenge deprotoniert als Anion vor, und ¾ als Zwitterion. In der HH-Gleichung würdest Du dann schreiben
pH = pK₂ + lg (Anion/Zwitterion) = pK₂ + lg (¼/¾) = pK₂ + lg(⅓)
Man sieht leicht, daß man das auch direkt über die Volumina schreiben kann:
pH = pK₂ + lg (V/(Vₑ−V)) = pK₂ + lg (10/(40−10)) = pK₂ + lg (10⁄30) = pK₂ + lg(⅓)
Das ist also nur eine flotte Schreibweise. Die Stoffmenge der gebildeten Base (also des Anions, blau in der ersten Graphik) steigt ja linear mit dem Verbrauch V an, und bei V=Vₑ=40 ml liegt alle Substanz als Base vor. Daher ist Vₑ−V proportional zur Stoffmenge an Zwitterion in der Lösung, und der Quotient aus beiden kann in die HH-Gleichung eingesetzt werden.
Der pH-Wert von 9,9 entspricht recht gut dem pKs der protonierten Aminofunktion der Aminosäure R-NH3⁺. Um diesen zu erreichen muss man eine äquimolare Stoffmenge an Hydroxyd-Ionen zu der neutralen Aminosäure (mit pH am IP) geben. Also:
n(NaOH⁻) = n(Alanin)
40 mL mit c = 0,1 mol/L sind n = 4 mmol Alanin
Also muss man 4 mmol NaOH dazu schütten. Mit n = c *V erhält man (Überraschung!) 40 mL NaOH mit 0,1 mol/L.
hätte vlt eine Frage. Wie stelle ich due gleichung denn um. ich erhalte bei meiner Rechnung immer noch keine 20 ml