Partialsumme für x^n?
Für einen Beweis brauche ich diese Partialsumme. Kann mir jemand sagen wie die lautet?
2 Antworten

Das Stichwort ist Harmonische Zahlen:

(siehe hier > Formel 31)
Bei dir ersetzt du k mit i und r mit k:
Wie du sie schreibst hängt von dir ab. Wie wäre es mit:
Geht n gegen unendlich, so erhältst du die riemannsche Zeta Funktion (das zweite in der Formel ist die Hurwitz bzw. Clasical Zeta Funktion).
Du kannst sie auch als Polygamma Funktion schreiben oder rekursiv schreiben...
Doch was du genau willst geht nicht hervor denn "Für einen Beweis brauche ich die Partialsumme. Kann mir jemand sagen wie die lautet?" ist da etwas ungenau, denn das ist bereits die n.te Paritalsumme.
ich möchte den folgenden Ausdruck beweisen:
lim n->unendlich (x/n*summe von i=1 bis n von (i/n * x)^k)
Das ist eine Formel ohne Relation, Behauptung oder Ähnliches zum Beweisen. Aber ich denke, dass du nur das Limit ziehen willst.
Es gilt:
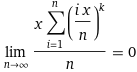
für k > 1.
Für k < 0 geht es gegen unendlich * sgn(x). Der Rest sind Spezialfälle...
Du kannst das n aus der Summe rausholen (da unabhängig von i). Du erhält:
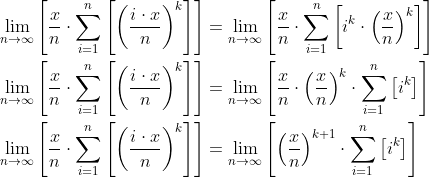
i^k haben wir uns schon davor hergleitet...
Geht n gegen unendlich so geht auch i^k gegen unendlich, wenn k <= 1. Ist k > 1, so ist das riemannsche Zeta Funktion (nur reelle Werte) aka wir können es so aus den Limit ziehen.
Ist k > -1, so geht der Bruch gegen 0. Für k > 1 geht der term also gegen 0, Für k < 0 gegen sgn(x^(k + 1)) * unendlich und für k in [0, 1] kommen nur Monome raus (nicht alle sind ganz-rational).
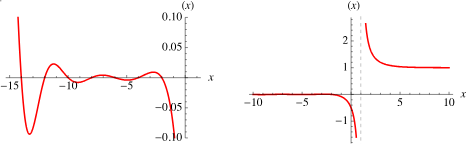
Plot von Zeta:
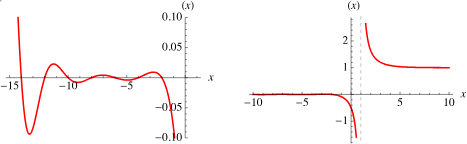
(nur x > 1 ist hier korrekt)
Beispiele von Monomen:
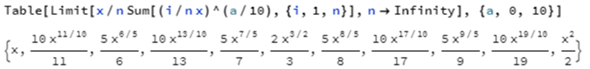
LaTeX-Code für interessierte:
\begin{align*}
\lim\limits_{n \to \infty}\left[ \frac{x}{n} \cdot \sum\limits_{i = 1}^{n}\left[ \left( \frac{i \cdot x}{n} \right)^{k} \right] \right] &=
\lim\limits_{n \to \infty}\left[ \frac{x}{n} \cdot \sum\limits_{i = 1}^{n}\left[ i^{k} \cdot \left( \frac{x}{n} \right)^{k} \right] \right]\\
\lim\limits_{n \to \infty}\left[ \frac{x}{n} \cdot \sum\limits_{i = 1}^{n}\left[ \left( \frac{i \cdot x}{n} \right)^{k} \right] \right] &=
\lim\limits_{n \to \infty}\left[ \frac{x}{n} \cdot \left( \frac{x}{n} \right)^{k} \cdot \sum\limits_{i = 1}^{n}\left[ i^{k} \right] \right]\\
\lim\limits_{n \to \infty}\left[ \frac{x}{n} \cdot \sum\limits_{i = 1}^{n}\left[ \left( \frac{i \cdot x}{n} \right)^{k} \right] \right] &= \lim\limits_{n \to \infty}\left[ \left( \frac{x}{n} \right)^{k + 1} \cdot \sum\limits_{i = 1}^{n}\left[ i^{k} \right] \right]\\
\end{align*}

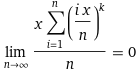
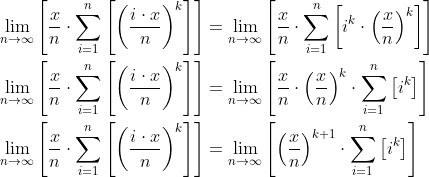
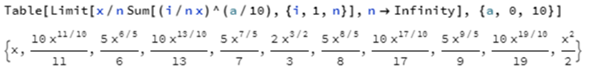

OK... Dann glaube ich, dass deine Summe falsch ist.
Ich kenne es als:
Int_{a}^{b}[ f(x) ] dx = lim_{Dx -> 0}[ Sum_{x = a}^{n}[ f(x) ] Dx ]
(siehe hier)
Wolfram|Alpha kann dir hier auch die Grenzwerte berechnen für deine Formel.
Eine ganz einfache Herleitung der Formel wäre (Zuerst schreibe ich die Formeln und dann die Übersetzung in Worte):
F'(x) = f(x) ∧ (f^{(n)}(x))' = f^{(n+1)}(x) => F(x) = f^{(-1)}(x)
f(x) = x^k
f'(x) = k * x^{k - 1}
f''(x) = k * (k - 1) * x^{k - 2}
f'''(x) = k * (k - 1) * (k - 2) * x^{k - 3} | Induktion
f^{(n)}(x) = k! / ((k - n)!) * x^{k - n}
f^{(-1)}(x) = k! / ((k - -1)!) * x^{k - -1}
f^{(-1)}(x) = k! / ((k + 1)!) * x^{k + 1}
f^{(-1)}(x) = k! / ((k + 1) * k!) * x^{k + 1}
f^{(-1)}(x) = 1 / (k + 1) * x^{k + 1}
F(x) = 1 / (k + 1) * x^{k + 1}

Übersetzung:
Die Ableitung der Stammfunktion von f ist f und die Ableitung der n.ten Ableitung von f ist die n+1.ste Ableitung von f, was impliziert, dass die Stammfunktion die -1.ste Ableitung wäre.
Die nullte Ableitung von x^k ist ...
Die erste Ableitung von x^k ist ...
...
Das lässt sich verallgemeinern zu f^{(n)}(x) = k! / ((k - n)!) * x^{k - n}.
(Beweis alternativ via natürliche Induktion möglich.)
Setzen wir -1 ein, so erhalten wir:
f^{(-1)}(x) = F(x) = 1 / (k + 1) * x^{k + 1}

Hier ist ein Screenshot von meinen Rechnungen. Vielleicht ist es damit verständlicher was genau ich machen will: https://prnt.sc/q0WlOM4eL7Ro

Hmm. Das ist schwierig, das allgemein anzugeben.
Für k = 1 gilt beispielsweise...
Für k = 2 gilt beispielsweise...
Für k = 3 gilt beispielsweise...
Für k = 4 gilt beispielsweise...
Bzw. ... Was genau meinst du damit, dass du die Partialsumme brauchst? Du kannst natürlich auch einfach...
... angeben. Das ist doch bereits die n-te Partialsumme. Gefällt dir diese Form nicht? Dann solltest du erläutern, warum dir diese Form nicht gefällt, und was die Form erfüllen soll, die du dir wünscht.

Ich möchte Beweisen, dass für das Integral von x^k 1/(k+1)*k^(k+1) gilt und dafür muss ich das Summenzeichen irgendwie auflösen können

Ich vermute mal, dass du 1/(k+1) * x^(k+1) statt „1/(k+1)*k^(k+1)“ meinst.
Hmm. An welcher Stelle brauchst du dann diese Partialsumme?
Habt ihr noch nicht den Hauptsatz der Differential- und Integralrechnung bewiesen. Denn mit Hilfe des HDI wäre das wirklich nicht schwer zu beweisen.

Ich möchte den folgenden Ausdruck beweisen:
lim n->unendlich (x/n*summe von i=1 bis n von (i/n * x)^k)
Uff das sieht wirklich kompliziert aus. Im Unterricht haben wir mit der summe (für werte von k wie z.B. 2 (also f(x)=x²) das Integral von der Funktion bestimmt. Das hat dann dazu geführt, dass man summe von i=1 bis n von i^2 hatte und für die Partialsumme gibt es ja einen Ausdruck den wir dann eingesetzt haben, alles aufgelöst haben und dann eben 1/3x³ rauskam. Mein Ziel war jetzt das ganze allgemein zu zeigen für f(x)=x^k dass dann davon das Integral F(x)=1/(k+1)*x^(k+1) ist.