Mechanik Aufgabe (schwer)?

Hat jemand einen Ansatz?

Answer 1

[mihisu]

Betrachte die Bewegung als Überlagerung zweier Bewegungen:

• in y-Richtung nach oben (bzw. bei negativer y-Richtung nach unten)
• in x-Richtung horizontal

Wenn man Reibungseffekte (Luftwiderstand, etc.) vernachlässigt, hat man dann in x-Richtung eine Bewegung mit konstanter Geschwindigkeit...

$x(t)=v_{x0}\cdot t$

$v_{x}(t)=v_{x0}$

Und in y-Richtung hat man einen senkrechten Wurf, bei der der Ball durch die Fallbeschleunigung konstant nach unten beschleunigt wird...

$y(t)=h+v_{y0}\cdot t-\frac{1}{2}\cdot g\cdot t^2$

$v_y(t)=v_{y0}-g\cdot t$

Die Anfangshöhe h = 80 m ist gegeben. Die Fallbeschleunigung beträgt in der Nähe der Erdoberfläche etwa g = 9,81 m/s². Für die anfänglichen Geschwindigkeitskomponenten muss man ein wenig rechnen...

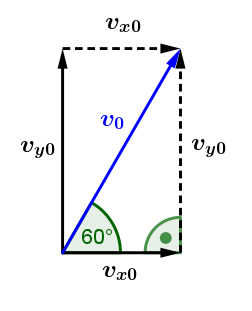
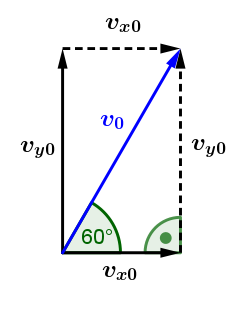
Versuche da mit etwas Trigonometrie (cos, sin, tan) mit der gegebenen Geschwindigkeit v[0] = 40 m/s und dem gegebenen Winkel 60° auf die Geschwindigkeitskomponenten v[x0] und v[y0] zu kommen.

============

Mit der Bewegungsgleichung...

$y(t)=h+v_{y0}\cdot t-\frac{1}{2}\cdot g\cdot t^2$

... kannst du dann die in Teilaufgabe a) gesuchte Zeit t berechnen, indem du die Gleichung y(t) = 0 nach t löst.

============

Mit ...

$v_{x}(t)=v_{x0}$

$v_y(t)=v_{y0}-g\cdot t$

... kannst du die Geschwindigkeitskomponenten für den in a) berechneten Zeitpunkt t bestimmen, indem du diesen Zeitpunkt einsetzt.

Den Geschwindigkeitsbetrag des Geschwindigkeitsvektors...

$\vec{v}=\begin{pmatrix}v_{x}\\ y_{y}\end{pmatrix}$

... erhält man dann mittels...

$\left\lvert \vec{v}\right\rvert=\sqrt{v_x^2+v_y^2}$

[Alternativ könnte man auch mit Energieerhaltung rechnen, dass die potentielle Energie in zusätzliche kinetische Energie umgewandelt wird.]

Answer 2

[Pixel7424]

a)

Betrag der Anfangsgeschwindigkeit in vertikale Richtung:

sin(60°) * 40m/s = 35m/s

Formel für y in Abhängigkeit von der Zeit t:

y(t) = 0.5 * a * t² + va * t

Einsetzen:

80m = 4,91m/s² + 35m/s * t

ohne Einheiten:

0 = 4,91 t² + 35 * t - 80

Nullstellen: x1 = -8,9; x2 = 1,8

Antwort: Er braucht 1,8 Sekunden.

b)

Endgeschwindigkeit beim Aufprall in horizontale Richtung (ist das gleiche wie die Geschwindigkeit in horizontaler Richtung zu Beginn des waagrechten Wurfs):

vx = cos(60°) * 40m/s = 20m/s

Endgeschwindigkeit beim Aufprall in vertikale Richtung:

vy = va + g * t = 40m/s + 9,81 m/s² * 1,8 s = 58m/s

Mittels des Satz des Pythagoras ergibt sich:

|v| = sqrt(vx² + vy²)

= sqrt((20m/s)² + (58m/s)²)

= 61m/s

Antwort: Die Aufprallgeschwindigkeit beträgt 61m/s.

Comments

[M4thematikus]

a) Ich glaube da bist du falsch

Es sind 8,9 s

[Pixel7424]

@M4thematikus

Entschuldigung, ich bin von einem Abwurfwinkel nach "unten" ausgegangen.