Mathematik Frage ergibt kein Sinn?
Lösung soll 25 quadratzentimeter sein, den Rechenweg gibt es bei den Lösungen nicht. doch es ergibt alles kein sinn? bitte hilfe.

Das grüne d war von mir weil ich zuerst die Diagonale rechnen wollte, aber das führte zu noch mehr verwirrung.
4 Antworten
d = √(12² + 4²) = √160
h = √((√160)² - 2²) = √156
A = (1 / 2) * 4 * √156
A = 25 cm² (gerundet)
Gegeben ist:
- AB, AC, BC und DE, DF, EF sind jeweils 4cm lang
- AD, BE und CF sind jeweils 12cm lang
Da du für die Berechnung der Fläche die Höhe des Dreiecks brauchst, müsstest du die Distanz von der Mitte der Strecke AB (Punkt c) zum Punkt C berechnen.
Dann kannst du mit dem Dreieck cCF die Höhe des gesuchten Dreiecks ermitteln.
Ich denke, dass Buch hat einen Fehler gemacht weil bei all meinen Durchgängen kommt immer ... A = 24cm^2 (mit Taschenrechner und alles) und deshalb denke ich, dass sich das Buch vertippt hat weil es anders ja nicht möglich sein kann.
Lösung soll 25 kubikzentimeter sein
"kubikzentimeter" macht keinen Sinn, da nach einer Fläche gefragt ist, nicht nach einem Volumen.
Da ABC und DEF gleichseitige Dreiecke sind, sind alle Seitenlängen dieser beiden Dreiecke: 4 cm.
d kannst du mit dem Satz des Pythagoras berechnen:
12² + 4² = d²
Für die Höhe vom Dreieck ABF musst du zuerst die Höhe vom Dreieck ABC mit Pythagoras berechnen und dann noch mal Pythagoras anwenden.
Dann kannst du die Fäche ausrechnen.
ich kommen auf exakt

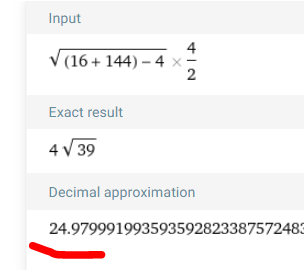
Warum -4² und nicht +4² ?
d ist doch die Hypotenuse und 12 und 4 sind die Längen der Katheten.