Mathe Hilfe zur Integralaufgabe im IV.Quadranten?
Gesucht ist die Fläche der Funktion f(x) =2sin(x)-2 die durch die beiden Koordinatenachsen im IV. Quadranten umschlossen wird.
Der IV. Quadrant ist x>=0 und y <=0
soll ich für die Integralgrenzen 0 bis unendlich festlegen ?
3 Antworten
Die Sinusfunktion ist periodisch. Und unterhalb der y-Achse, bzw im 4. Quadranten kommen immer wieder neue, gleich große Flächen dazu. Der Flächeninhalt ist also unendlich. Mit Integrationsgrenzen von 0 bis unendlich hast du das Problem, dass sich positive und negative Flächen gegenseitig auslöschen.
zeichne zuerst mal f(x)=2*sin(x) mit deinen Graphikrechner (GTR) falls du einen hast
dann um 2 Einheiten nach unten verschieben → f(x)=2*sin(a)-2
wir sehen: 1.tes Maximum bei x=pi/2 hier berührt der Graph die x-Achse
Integrationsgrenzen untere Grenze xu=0 und obere Grenze xo=pi/2
F(x)=∫(2*sin(x)-2)*dx=2*∫sin(x)*dx-2*∫dx=2*(-1)*cos(x)-2*x+C
F(x)=-2*cos(x)-2*x+C
A=obere Grenze minus untere Grenze → xo=pi/2 und xu=0
A=(-2*cos(pi/2)-2*pi/2) - (-2*cos(0)-2*0)=(-pi) - (-2)=-pi+2
A1=-1,146 FE (Flächeneinheiten)
weiter sehen wir eine weitere Fläche unter der x-Achse zwischen den x-Werten
xu=pi/2 und xo=5/2*pi
A2=(-2*cos(5/2*pi)-2*5/2*pi) - (-2*cos(pi/2)-2*pi/2)=(-5*pi) - (-pi)
A2=-4*pi FE=-12,566..FE (Flächeneinheiten)
A2 wiederholt sich dann periodisch.
y=f(x)=sin(x)
Nullstellen bei x=k*pi → k=0,1,2,3...
Extrema bei x=pi/2+k*pi → k=0,1,2,3...
Wendepunkte x=k*pi → k=0,1,2,3...
dann sollte die Fläche auch unendlichsein.........Wolfram sagt : fläche konvergiert nicht.
man kann aber mE
int von 0 bis erste NSt und dann von erster bis zweiter NSt usw , wiederholt sich ja
bilden und das so auf schreiben : Int1 + n*(int von Nst 2 bis Nst 3 )
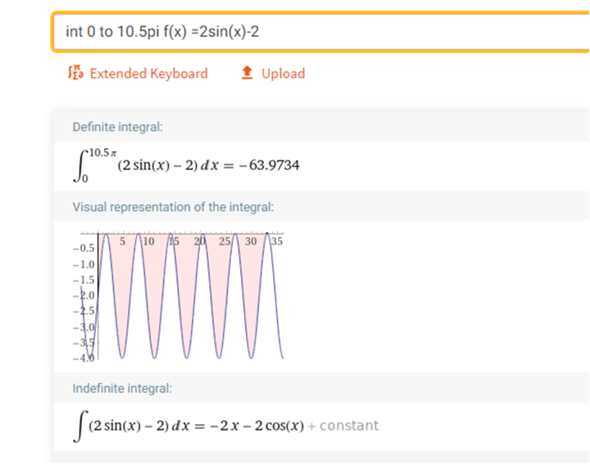
das ist das integral
-2 x - 2 cos(x)..............setzt man für x unend ein , wird es -2 * "unend" , also negativ unend , da die Fläche UNTER der -Achse liegt
cos(x) kann max +1 oder -1 werden , also zu vernachlässigen.
hier aber kein auslöschen
https://www.wolframalpha.com/input/?i=f%28x%29+%3D2sin%28x%29-2+