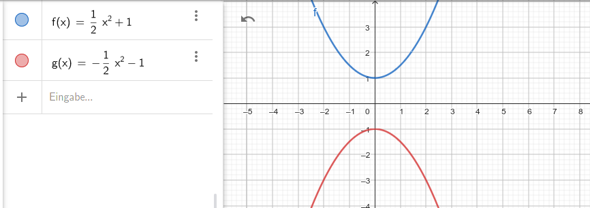
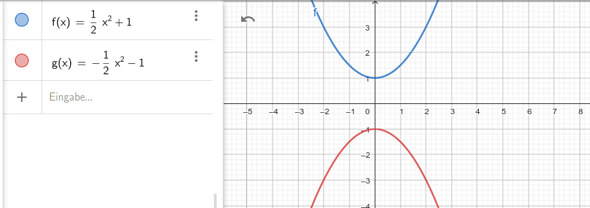
Mathe?

Kann mir einer bei der Aufgabe c helfen

Answer 1

[Rhenane]

In der Funktionsgleichung y=ax²+b hast Du zwei unbekannte Parameter (a und b), d. h. Du benötigst 2 Punkte, um diese Funktion eindeutig bestimmen zu können. "Grafisch" handelt es sich bei y=ax²+b um eine Parabel, die nur auf der y-Achse verschoben wurde. Das b bestimmt in diesem Fall die Verschiebung in y-Richtung und ist hier eindeutig ablesbar, Punkt (0|1), also b=1.

Jetzt liest Du noch einen weiteren eindeutig erkennbaren Punkt ab (z. B. (2|2)) und setzt diesen in die Gleichung ein und löst nach dem noch unbekannten Streckungsfaktor a auf, also 2=a*2²+1 nach a umstellen.

Answer 2

[evtldocha]

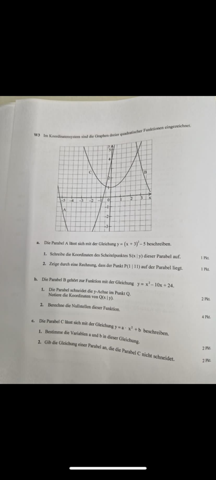
Aufgabe a 1.) Nur aus der Gleichung ablesen: S(x | y) = S( -3 | -5)

Aufgabe a 2.) y(1) = (1 + 3)² - 5 = 4² - 5 =16 - 5 = 11. Damit liegt P(1 | 11) auf der Parabel

Aufgabe b 1.) Schnittpunkt mit der y-Achse heißt: x=0. Damit y = 0² -10·0 + 24 = 24. Damit Q(x | y) = Q(0 | 24)

Aufgabe b 2.) Dazu schreibt man die Gleichung etwas um
$y=x^2-10x+24\ =\ \left(x-4\right)\cdot\left(x-6\right)$

Nun kann man die Nullstellen mit dem Satz vom Nullprodukt direkt ablesen:

$x_1=4;\ x_2=6$

Aufgabe c 1.) Die Funktionsgleichung kann man ablesen oder mit

$f\left(0\right)=1;\ f\left(1\right)\ =\ \frac{3}{2}$ berechnen

$y=\frac{1}{2}x^2+1;\ a=\frac{1}{2};\ b=1$

Aufgabe c 2.) Da mach mach ich mir jetzt das Leben einfach und spiegele die Parabel an der y - Achse (y → - y)

$y=-\frac{1}{2}x^2-1$