Mathe?

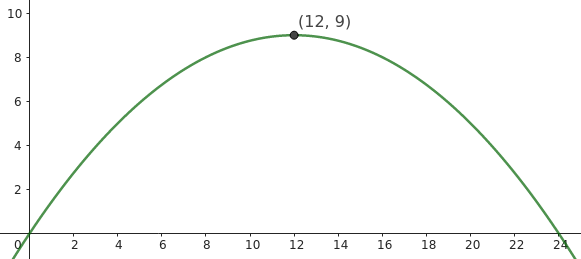
"Der Bogen einer Stahlbrücke kann durch den Funktionsterm f(x)=-1/16(x-12)²+9 beschrieben werden. Ändere die Gleichung der Parabel so ab, dass der Bogen 12m hoch ist und die Spannweiteerhalten bleibt."

Wie geht man da vor?

Answer 1

[SebRmR]

f(x) = -1/16•(x - 12)² + 9
Ist die Scheitelpunktform einer Parabel. Der Scheitelpunkt liegt bei (12|9) [Skizze grüne Parabel].

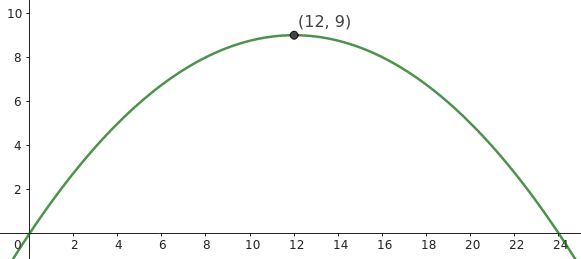
Wenn der Scheitelpunkt eine Höhe von 12m haben soll, also (12|12), muss man in der Scheitelpunktform (den Zusammenhang zwischen Scheitelpunkt und Scheitelpunktform kennst du?) "am Ende" was ändern. Hier: aus +9 muss +12 werden:

f(x) = -1/16•(x - 12)² + 12
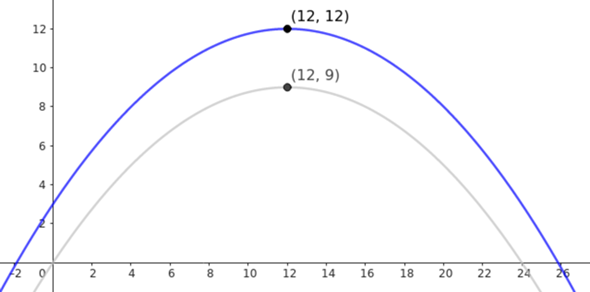
Diese Parabel sieht so aus [blau, als Vergleich grau die ursprüngliche]

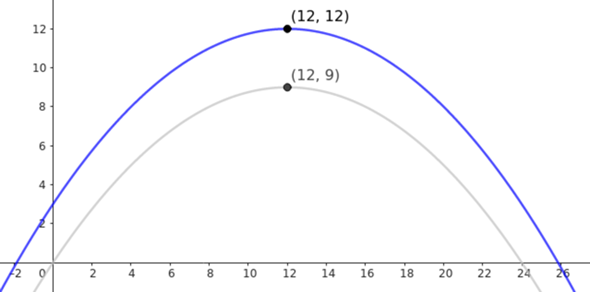
Man sieh zwei Sachen:
Die Höhe ist wie gewünscht und erwarten 12.
Aber die Spannweite hat sich verändert.

Die Spannweite ist der Abstand der Nullstellen.
Ursprünglich war die Spannweite 24, Nullstellen (0|0) und (24|0).
Die "neue Parabel" hat eine größere Spannweite von 28.
Um die Spannweite, also die Nullstellen zu verändern, muss man den Faktor (im folgenden a) vor der Klammer verändern (Stichworte: Streckung, Stauchung). Die Parabel muss "schmaler" werden. Die Nullstellen sollen wieder (0|0) und (24|0) lauten

f(x) = a•(x - 12)² + 12
Um a zu bestimmen, eine der Nullstellen einsetzen. Ich würde (0|0) nehmen:
0 = a(0 - 12)² + 12
a sollte zu berechnen sein. a kann man schön als Bruch schreiben.

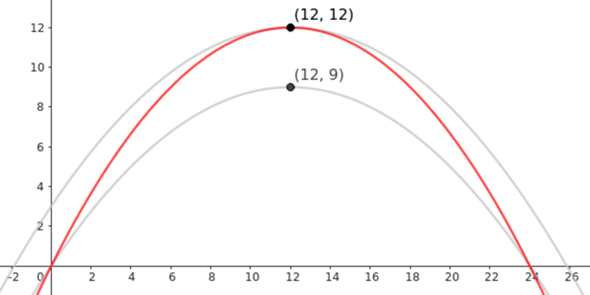
Mit dem richtigen a erhält man die rote Parabel:

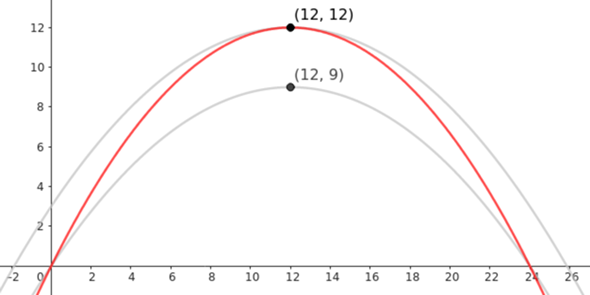
Wie man sieht, die Höhe passt und auch die Spannweite/Nullstellen