Kurvendiskussion: Kann f(x)= 4xe^(-0,5x)+36,6 überhaupt eine Nullstelle haben?
In Mathe haben wir momentan das Thema Kurvendiskussion. Wir sollen von verschiedenen Funktionen die Nullstelle berechnen. Kann f(x)= 4x*e^(-0,5x)+36,6 eine Nullstelle haben ?Ich komme auf x=-9,15, das Ergebnis scheint aber falsch zu sein.
Ich wäre über eure Hilfe dankbar.
6 Antworten
Ja !
An der Stelle für x an der 4 * x * e^(-0,5 * x) den Wert -36,6 annehmen würde, könnte eine Nullstelle sein.
Ob das auch wirklich der Fall ist, das können wir mal ausprobieren -->
4 * x * e ^ (-0.5 * x) = -36.6 | : 4
x * e ^ (-0.5 * x) = -9.15
9.15 + x * e ^ (-0.5 * x) = 0
Nun führen wir eine Hilfsfunktion ein -->
h(x) = 9.15 + x * e ^ (-0.5 * x)
und bilden auch sofort die 1-te Ableitung -->
h´(x) = (1 - 0.5 * x) * e ^ (-0.5 * x)
Nun Stellen wir eine Wertetabelle für h(x) auf -->
Anhand der Wertetabelle auf der Webseite können wir sehen, dass sich zwischen x = -3 und x = -2 eine Nullstelle befinden muss, weil es dort zu einem Vorzeichenwechsel von - nach + kommt. Weil der Absolutwert von h(x) an der Stelle x = -2 kleiner ist, als an der Stelle x = -3, ist der Näherungswert x = -2 geeigneter.
Nun wenden wir das Newton-Verfahren an.
https://de.wikipedia.org/wiki/Newton-Verfahren
Das Newtonverfahren läuft folgendermaßen ab -->
1.) Wähle einen Startwert für x, den kannst du anhand einer Wertetabelle oder einer Zeichnung der Funktion erhalten.
2.) Berechne -->
z= x - h(x) / h´(x)
3.) Vergleiche z und x miteinander, wenn sie sich zu stark von einander unterscheiden, dann mache weiter, wenn nicht dann springe zu 6.)
4.) Setzte x = z
5.) Springe zu 2.)
6.) Setze x = z
7.) x ist das Endergebnis, beende den Algorithmus jetzt.
Für das Newtonverfahren brauchen wir die zu untersuchende Funktion, die 1-te Ableitung dieser Funktion und einen Startwert.
Das haben wir alles.
h(x) = 9.15 + x * e ^ (-0.5 * x)
h´(x) = (1 - 0.5 * x) * e ^ (-0.5 * x)
Startwert x = -2
Mit dem Startwert x = -2 erhalten wir nach 5 Iterationen den Wert
x = -2.55298288772328An der Stelle befindet sich deine Nullstelle.
Ja, das kann man natürlich ebenfalls machen.
In beiden Fällen kommt ein identisches Ergebnis heraus.
Das mit den -36.6 habe ich genommen, weil es das Gegenstück zu +36.6 ist, weil der Fragesteller gefragt hat, ob es überhaupt Nullstellen geben kann, und es dadurch logisch ist, dass es welche geben kann.
Hallo,
diese Funktion kann nicht nur eine Nullstelle haben, sie hat auch eine bei x=-2,553. Zu berechnen geht das am besten durch ein Näherungsverfahren wie das Newton-Verfahren oder durch eine Wertetabelle.
Die e-Funktion selbst wird zwar niemals gleich oder kleiner als Null, hier wird sie aber mit 4x multipliziert. Wenn x negativ ist, kann die Funktion durchaus negativ werden. Diese wird und bleibt negativ für alle x kleiner als -2,553.
Herzliche Grüße,
Willy
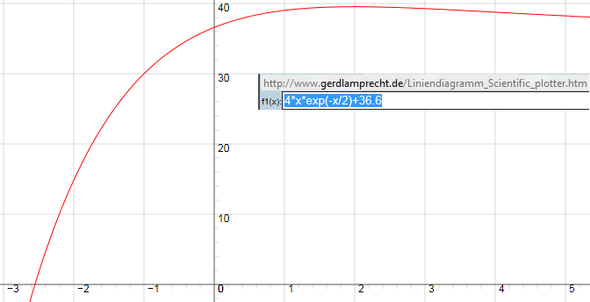
Vor der Exp-Funktion steht ein "Mal x" das natürlich - egal bei welchem festen Offset - irgendwann zu 0 "runterdrückt" siehe Plott - Bild
Natürlich hattet Ihr in der Schule keine LambertW-Funktion, sondern probiert mit Näherungslösungen wie
- grafisch ablesen
- Newton-Iteration
- Bisektion
Aber als Mathe-Experte hier die 4 exakten Lösungen:
4*x*exp(-x/2)+366/10=0
4x*exp(-x/2)=-366/10 |/4
x*exp(-x/2)=-366/40
gehört zum Aufgabentyp
http://www.lamprechts.de/gerd/LambertW-Beispiele.html
§6 mit a=-1/2, b=-366/40, p=0, h=1
x=h/a * LambertW(n, a/h * (-1)^(2*N/h) * (b/e^p)^(1/h)) ; n=-2...1
x=-2 * LambertW(n,-1/2 * (-1)^(2*N) * (-366/40))
x=-2 * LambertW(n,-1/2 * (-1)^(2*N) * (-366/40))
x=-2 * LambertW(n,183/40)
n | x 4 Lösungen:
-2 | 1.74557956845259857757595759+21.831574753841019268216043 i
-1 | 0.05665661479094891000187500+9.41273982274614478721407781 i
0 | -2.55298288772327993586607570
1 | 0.05665661479094891000187500-9.41273982274614478721407781 i
Probe (bei komplexen Ergebnissen immer wichtig!):
alle 4 x in Ausgangsformel ergeben 0 -> OK
P.S.: alle guten Rechner (wie der im LINK) kennen die LambertW-Funktion
und ohne den 1. Parameter schreiben viele kurz:
W(x)=LambertW(0,x)
Wolfram Alpha sagt ja:
http://www.wolframalpha.com/input/?i=Zeros[4*x*e^%28-1%2F2*x%29%2B36.6]
scheint aber ohne weiteres nicht sehr einfach zu berechnen zu sein. Wüsste leider gerade auch nicht welche Tricks man da anwenden muss.
lg
kannst doch die Probe machen und deinen Wert für x einsetzen;
ansonsten musst du dich annähern und gucken, ob Vorzeichenwechsel kommt.
Ich habe direkt mit dem Newton-Verfahren gerechnet ohne Hilfsfunktion. Funktioniert auch. Praktisch ist da immer eine Tabellenkalkulation.
Herzliche Grüße,
Willy