Kondensator und Spule im Schwingkreis?
Hallo, im eigenen Interesse habe ich eine Frage zur Umpolung des Kondensator im Schwingkreis.
Wenn der Kondensator sich entlädt induziert er eine Spannung in der Spule, welche den Entladungsvorgang nach der Lenzschen Regel hemmt und diesen fast konstant ablaufen lässt.
Wie kommt es jetzt aber zur Umpolung wenn der Induktionsstrom entgegen wirkt und sich der Kondensator nur bis zur Neutralität entlädt. Wenn der Kondensator wieder einen entgegengesetzten Ladungsschwerpunkt erzeugen würde bräuchte man die Spule doch nicht, aber das macht ein Kondensator ja auch nicht.
Also: Wie entsteht die Umpolung und welche Rolle spielt die Spule?
Danke!
4 Antworten
Wenn C vollständig entladen ist (U=0), fließt der größte Strom I. Dieser kann aber dann nicht plötzlich Null werden, da die Induktivität sich gegen Stromänderungen mit einer Induktionsspannung wehrt:
U = L dI/dt
Daher muss I noch weiterfließen - und zwar so lange bis C umgekehrt aufgeladen ist. Damit wiederholt sich das Spiel.
Vergleiche mit einer Kinderschaukel: Die Schaukel bleibt am tiefsten Punkt ja auch nicht stehen, sondern erreicht den gegenüberliegenden (=negativen) Punkt.
Kannst du mit
Uind = L dI/dt
etwas anfangen?
Hattest du in der Schule schon Differentialrechnung?
sie hemmt nicht den Stromfluss an sich , sondern sie hemmt Änderungen des Stromes.
Ja ich hab heute Physikabi geschrieben, der Kondensator kam nicht dran. Wenn du sagst die Spule hemmt die Änderung also das erliegen des Stromflusses scheint mir das logisch wieso der Kondensator entgegengesetzt aufgeladen wird, doch wieso wird die ÄNDERUNG gehemmt, uns wurde die Hemmung des Stromflusses erklärt da die induzierte Spannung dem Kondensatorstrom entgegenwirkt und gerade deshalb das erliegen fördert. Wird der Kondensatorstrom weniger wird erneut durch die Änderung des elektrischen Feldes die Spannung induziert, die aber diesmal das sich das Feld abbaute, in Richtung des Kondensatorstroms wirkt und dadurch den Stromfluss vom vollständigen erliegen abhält bis die Umpolung geschenen ist. Meinst du das mit "die Änderung wird gehemmt" ?
Du vermischst da noch immer die 4 Phasen im Schwingvorgang zwischen Kondensator und Spule. Deshalb kann man darauf kaum antworten. Nur soviel:
- Abgeschalteter Strom möchte sich grundsätzlich unendlich schnell ändern (nämlich "digital" von 1 auf 0, Vollbremsung). Beim Widerstand geht das.
- Bei der Spule nicht. Da wird durch das Zusammenbrechen des Magnetfeldes eine Spannung induziert, die in allem, was angeschlossen ist, einen Stromfluss erzeugt, der danach aussieht, als fliesse der Strom "aus der Spule" wie aus einer Quelle weiter.
- Somit wird die unendlich schnell sein wollende Aenderung gehemmt, die Aenderung läuft damit "langsamer" ab. Wenn ein Widerstand angeschlossen wäre, wird diese Energie verheizt, der Abfall ist dann eben exponentiell.
- Weil ein Kondensator angeschlossen ist (der ein Energiespeicher ist), übernimmt er diese Energie. Wenn die Spule entladen ist (bzw. schon vorher), ist sie für den Kondensator wieder eine Bremse, der Kondensator kann das Magnetfeld in der Spule nicht unendlich schnell aufbauen.
- Die dauernde Überlagerung all der auf- und abfallenden Exponentialkurven ergibt dann eben die Sinusschwingungen.
Der Kondensator macht den "entgegengesetzten Ladungsschwerpunkt", und zwar wegen der Spule.
Der Kondensator entlädt sich eben nicht nur bis zur Neutralität, sondern wird durch den noch andauernden Strom in der Spule wieder gegenpolig aufgeladen.
Schau dir diese Animation an (Zeitlupe 100x):
Noch als Ergänzung:
- man spricht nicht von Induktionsstrom, sondern von induzierter Spannung. Diese tritt solange auf, wie sich der Strom in der Induktivität ändert.
- Du fragst:Wie wehrt sich die Induktivität mit einer Spannung gegen die Änderung. Ich dachte die Induktionsspannung hemmt gerade den den Stromfluss. - Wehren und hemmen heisst nur "bremsen" aber nicht verhindern!
- Über das Einschalten von Spulen weisst du wohl Bescheid. Sonst schau auch hier: http://www.leifiphysik.de/elektrizitaetslehre/elektromagnetische-induktion/ein-und-ausschalten-von-rl-kreisen
Wenn du das Abi geschrieben hast, wirst du nicht mehr interessiert daran sein, aber:
aus dem Maschensatz ergibt sich
dI/dt =-1/L * Uc
Die Änderungsrate des Stromes ist also proportional zur negativen Kondensatorspannung.
D.h. wenn Uc negativ ist, fließt Strom in den Kondensator hinein, umgekehrt fließt Strom heraus. Wenn Uc=0 ist, hat I seinen Maximalwert.
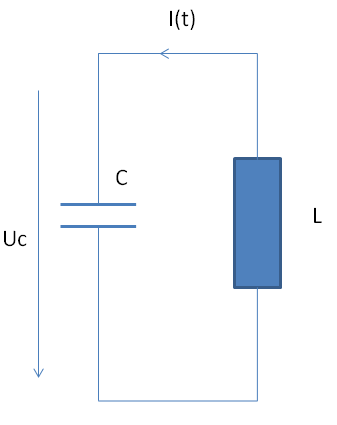
Ich will versuchen, den Ablauf des Schwingungsvorgangs anhand einzelner Etappen zu erklären.
Der Schwingkreis ist zunächst unterbrochen. Der Kondensator C ist auf die volle Spannung Uo aufgeladen, die Spule L ist stromlos.
Zeitpunkt 1: t=0. Durch einen Schalter wird C mit L verbunden. An L liegt zunächst die Spannung Uo. Sie bewirkt gemäß Ul = L*di/dt einen schnellen Stromanstieg im Schwingkreis, Dadurch sinkt allmählich die Spannung Uc an C und damit auch die Spannung Ul an L, was wiederum den Stromanstieg di/dt kleiner werden lässt; der Strom steigt aber weiter an.
Zeitpunkt 2: t=pi/4. Der Kondensator C hat durch den Stromabfluss nun schon deutlich weniger Ladung. Entsprechend ist Uc deutlich kleiner und damit auch di/dt deutlich kleiner. Aber der Strom i wächst immer noch.
Zeitpunkt 3: t=pi/2. C ist jetzt voll entladen. Uc=0, di/dt =0, der Strom wächst nicht mehr, er hat seinen Maximalwert erreicht. Die gesamte Energie, die zum Zeitpunkt t=0 in der Ladung des Kondensators gesteckt hat, ist nun im Magnetfeld der Spule L gespeichert. Würde man nun die Spule kurzschließen (beide Spulenanschlüsse mit einem dicken Draht verbinden), dann würde der Strom noch lange weiter fließen. Bei Abkühlung von Spule und Verbindungsdraht auf sehr niedrige Temperatur, so dass Supraleitung einsetzt, würde dieser Stromfluss unbegrenzt aufrecht erhalten.
Zeitpunkt 4: t=(3/4)pi. Da der Stromfluss in der Spule weiter gelaufen ist, ist nun C "verkehrt herum" teilweise aufgeladen worden. Dadurch ist Uc von 0 auf einen negativen Wert "angestiegen". Dieser negative Spannungswert ist gegen den Stromfluss gerichtet und bewirkt ein negatives di/dt, d.h. der Strom wird verringert. Das Magnetfeld von L wird langsam abgebaut, während die Ladung in C aufgebaut wird.
Zeitpunkt 5: t=pi. Der Strom i ist nun zu 0 geworden. Das Magnetfeld der Spule L ist verschwunden. Die gesamte Energie steckt jetzt wieder in der (allerdings "negativen") Ladung des Kondensators C, der jetzt die Spannung Uc = -Uo aufweist. Zeitpunkt 5 entspricht Zeitpunkt 1, nur mit umgekehrtem Vorzeichen. Nun beginnt das Spiel mit umgekehrtem Vorzeichen von neuem. Zum Zeitpunkt 9, t=2pi wäre dann wieder der Ausgangszustand von Zeitpunkt 1 mit den gleichen Vorzeichen erreicht.
Insgesamt schwingt also die Energie von der Ladungsenergie des Kondensators zur Magnetfeldenergie der Spule und wieder zurück zur Ladungsenergie des Kondensators und immer so weiter. Daher die Bezeichnung Schwingkreis.
Das physikalische Analogon hierzu ist das mechanische Pendel (Schaukel). Auch hier schwingt im Bewegungszustand die reine Lageenergie des seitlich aus gelenkten Pendels über die reine Bewegungsenergie im Tiefpunkt der Pendelbewegung wieder zur reinen Lageenergie des zur anderen Seite geschwungenen Pendels auf dessen Höhepunkt und immer so weiter.
Danke für deine Antwort,
wie kann ich mir das vorstellen: Die Induktivität wehrt sich mit einer Spannung gegen die Änderung.
Ich dachte die Induktionsspannung hemmt gerade den den Stromfluss.