Komplexe Zahlen in Polarform?
Hallo,
ich habe die Aufgabe bekommen, diese Darstellungen zweimal in Polarkoordinaten darzustellen. Leider finde ich mich da nicht richtig zurecht.
Ab den Pfeilen blicke ich echt nicht mehr durch, wir haben gesagt, dass
e^{π/6i}
unser Ergebnis ist, was auch sein mag, da unser Winkel
φ = π/6 = 30°
ist. Nun verstehe ich nicht ganz, wieso man weiter den Winkel beschreibt und sagt, der ist
φ = –π/6 + 2πK,
woher kommt das überhaupt? Und wie kommt man dann im nächsten Schritt von diesem Ergebnis auf die beiden Lösungen am Ende?

3 Antworten
Mit 360° = 2 π läufst du einmal um den Kreis herum. Die trigonometrischen Funktionen wiederholen sich dann.
2 π k bedeutet k Kreisumläufe.
Durch einen Richtungspfeil bzw. durch Sinus und Kosinus ist ein Winkel also nur modulo 2 π bestimmt (d. h. bis auf ein ganzzahliges Vielfaches von 2 π).
Wegen der Euler-Identität ( https://de.wikipedia.org/wiki/Eulersche_Formel ) ist auch e^(2 π i) = 1 und e^(i φ) 2-π-periodisch in φ.
In der Aufgabe geht es nun darum, durch Addition / Subtraktion ganzzahliger Vielfacher von 2 π den Winkel in das jeweils geforderte Intervall zu bringen.
k ist -- wie gesagt -- eine ganze Zahl. Also 0, +1, -1, +2, -2, ...
Entweder probierst du durch, oder du rechnest k = Boden(φ / (2 π))
(wobei Boden die Gaußklammer-Funktion ist, die jeder Zahl die größte ganze Zahl zuordnet, die nicht größer als die gegebene Zahl ist (von engl. floor -- so heißt die Funktion dort))
Hallo Isakoch,
Ab den Pfeilen blicke ich echt nicht mehr durch, wir haben gesagt, dass e^{π/6i} unser Ergebnis ist,…
Ja, wobei dies mit e^{–i·π/6} identisch ist.
…was auch sein mag, da unser Winkel φ = π/6 = 30° ist.
Nein, es wäre
φ = –π/6 = –30°,
wobei die Pseudo-Maßeinheit „Grad“ in diesem Zusammenhang keinen Sinn ergibt. Exponenten müssen dimensionslos sein, und dasselbe gilt für eine Variable φ, deren Funktion man in eine Potenzreihe entwickeln kann.
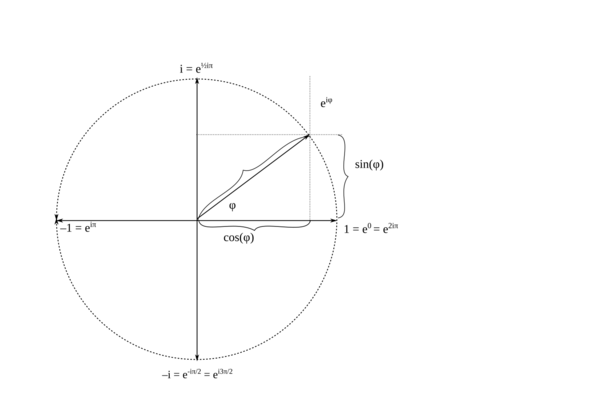
Die Polardarstellung der Komplexen Zahlen beruht auf
(EULER) e^{i·φ} = cos(φ) + i·sin(φ),
deren tieferer Grund in den Eigenschaften der Exponentialfunktion und der trigonometrischen Funktionen liegt, genauer in den Ableitungsfunktionen (also der Funktion, die jedem φ-Wert die Tangentensteigung zuordnet, falls es eine gibt, und der Ableitung der Ableitung usw.).
Die der Exponentialfunktion ist diese selbst, und wenn man –φ einsetzt, ist sie das Negative davon. Die zweite Ableitungsfunktion der Exponentialfunktion, und zwar auch von e^{–φ}, ist wieder sie selbst.
Bei den trigonometrischen Funktionen landet man nach zweimaligem Ableiten erst mal beim Negativen, und dasselbe sollte passieren, wenn man in der Exponentialfunktion als Argument i·φ einsetzt.
Auch an den Potenzreihendarstellungen kann man (EULER) erkennen, was damit natürlich zusammenhängt.
Der Vorteil dieser Darstellung ist, dass sich z₁=r₁·e^{iφ₁} sehr viel leichter, auch dank der Potenzgesetze, nicht nur mit einer anderen Komplexen Zahl z₂=r₂·e^{iφ₂} multiplizieren,
z₁z₂ = r₁r₂·e^{i·(φ₁ + φ₂),
sondern auch durch sie dividieren,
z₁/z₂ = r₁/r₂·e^{i·(φ₁ – φ₂),
aber auch potenzieren,
zⁿ = rⁿ·e^{i·n·φ} (n muss keine natürliche und nicht einmal eine rationale Zahl sein),
radizieren und für z≠0 auch logarithmieren lässt (dazu kommen wir noch).
φ = –π/6 + 2πK, woher kommt das überhaupt?
Die Exponentialfunktion mit rein imaginärem Argument und die trigonometrischen Funktionen sind 2π-periodisch, und deshalb ist
e^{iφ} = e^{i·(φ + 2kπ)}, k ∈ ℤ.
Bei der Ziehung der n. Wurzel gibt es daher im Prinzip n Lösungen, beim Logrithmieren sogar abzählbar unendlich viele, sodass man einen Wert als „Hauptwert“ auswählen muss. Es ist zunächst einmal
ⁿ√{z}ₖ = ⁿ√{r}·e^{i·(φ/n + 2πk/n)}, k ∈ ℤ, –π < φ ≤ π
und
lnₖ(z) = ln(r) + k·i·φ, k ∈ ℤ,
und der Hauptwert ist der mit k = 0.
Deine Frage ist nicht klar und in holpriger Sprache formuliert. Wenn ich Dich verstanden habe, dann ist der Dir fehlende Hinweis: Der Exponent des ersten e-Terms für z wird mit dem für die Klammer gefundenen e-Term verglichen. Daher die Formel am ersten Pfeil. k wird wg. der Mehrdeutigkeit der Kreisfunktion benötigt. Und dann die kleinsten Werte für die Lösung angegeben.
Aber was ist denn nun eingesetzt worden für k ,damit e hoch 11pi*i/6 raus kommt ?
einfach irgendwelche zahlen von den intervallen ,welche oben angegeben sind?