Kann mir jemand bei dieser Aufgabe helfen?
Hallo,
ich habe eine Frage bezüglich einer Aufgabe. Es sind keine Hausaufgaben. ;)
Mir würde es schon reichen, wenn man mir einen Rechenansatz gibt.
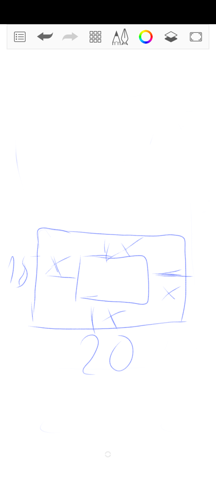
Bens Eltern möchten im Garten einen Swimmingpool bauen. Zur Verfügung steht eine Rasenfläche von 20 m Breite und 15 m Länge, von der aber 2/3 Rasen bleiben soll. Um den Pool soll an allen Seiten gleich viel Rand bleiben.
Wie viel Rand bleibt an den Seiten?
Löse mit der pq-Formel!
2 Antworten
Entweder mit:
Fläche von Pool:
A1=(15-2x)*(20-2x)=1/3 *20*15
oder mit:
Fläche vom Rasen um Pool:
A2=2*15*x+2*(20-2x)*x=2/3 *15*20

A1=300-30x-40x+4x^2=100
4x^2-70x+200=0
x1/2=(70+-Wurzel((-70)^2-4*4*200))/(2*4)
x1=3.596(gerundet)
(x2=13.904)(kann nicht die Lösung sein)
Es haben zwei Klammern gefehlt, eine um den gesamten Zähler und eine um den Nenner. Das Weglassen der Klammern macht bei einem Bruch halt schon einen Unterschied.
Ich habe ja auch nur darauf hingewiesen, damit der Fragesteller nicht noch zusätzlich verwirrt wird.
Dasselbe mit dem Hinweis auf die pq-Formel.
Meiner Meinung nach ist es hier nicht besonders sinnvoll, die zu nehmen, weil man sonst mit Brüchen in der Wurzel jonglieren muss, aber es soll ja wie gesagt dem Fragesteller geholfen werden.
Du musst doch nur ein Rechteck gleichmäßig aufteilen. Das heißt wie weit bist du bisher selbst gekommen? Dann schauen wir Mal wie man dir weiter helfen kann!
Prinzipiell der richtige Ansatz, aber der Fragesteller sollte ja die pq-Formel benutzen. Ist hier zwar nicht ideal, aber wenn's gefordert ist...
Aber bitte, bitte, setze doch noch Klammern um die Lösung. So, wie es jetzt dasteht, ist das ja echt gruselig.
( 70+-Wurzel((-70)^2-4*4*200) ) / (2*4)
Oder noch besser so, zum besseren Lesen: x₁₂ = (70 ± √((-70)² - 4⋅4⋅200)) / (2⋅4)
😉