Innenwinkel eines Trapez berechnen?
Hey!
Ich bin in der 10. Klasse und ein Klassenkamerad hat folgende Aufgabe rausgesucht, welcher keiner von uns lösen konnte.
Also
Das einzige was Gegeben war, sind die folgenden Seitenbezeichnungen im Bild und dass es symmetrisch ist
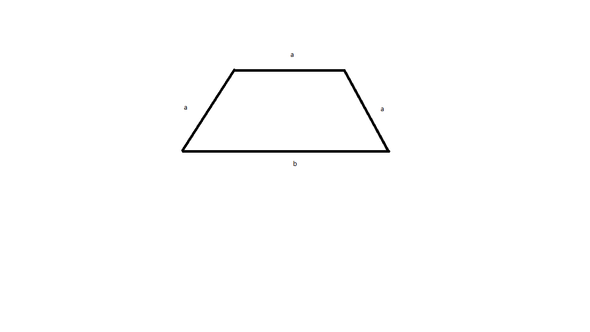
6 Antworten

Isoliere in diesem Bild ein rechtwinkeliges Dreieck.
Ermittle, wie lang dessen Seiten sind. Wenn du von der oberen rechten Ecke z.B. eine Senkrechte runterziehst, dann ergibt sich ein rechtwinkeliges Dreieck.
Die Hypothenuse ist dabei so lang wie a,
die untere, kurze Kathete hat die Länge (b-a)/2
die lange Kathete kannst du dir mit dem Satz des Pythagoras herleiten.
Somit hast du die Seitenverhältnisse des Dreieckes und kannst nun die trigonometrischen Formeln anwenden, um die Winkel zu ermitteln.
Du brauchst allerdings nur den Winkel unten rechts. Der Winkel oben rechts ergibt sich aus der Z-Formel.
Und um ganz sicherzugehen addierst du zum Schluss alle vier Winkel und musst dabei auf 360° kommen.


Ziehe einfach eine Mitteldiagonale von der linken unteren zur rechten oberen Ecke.
Dann hast du zwei Dreiecke mit einer gemeinsamen Seite.
Jetzt nimmst du einfach den Kosinussatz und kannst allgemein die Länge der Diagonalen berechnen:
d² = a² + b² - 2ab*cos(alpha) (alpha ist der Basiswinkel).
Aber was auch gilt: a² + a² + 2a*a*cos(beta) = d²
Da beide Gleichungen beta ergeben, erhältst du also
a² + b² - 2ab*cos(alpha) = 2a² - 2a²cos(beta)
Jetzt wissen wir aber zusätzlich noch, dass 2alpha + 2beta = 360° sind.
Daraus folgt für beta:
beta = 180° - alpha
Deswegen ist die rechte Seite der Gleichung 2a² - 2a²*cos(180°-alpha)
Aber es gilt noch ein weiterer Satz: cos(x) = -cos(180°-x)
Somit ist cos(180°-alpha) = -cos(alpha)
Und unsere Gleichung lautet:
a² + b² - 2ab*cos(alpha) = 2a² - 2a²*-cos(alpha) <=> a² + b² - 2ab*cos(alpha) = 2a² + 2a²cos(alpha)
Jetzt ziehen wir erst mal 2a² auf jeder Seite ab und erhalten:
b² - a² - 2ab*cos(alpha) = 2a²cos(alpha) <=> b² - a² = (2a²+2ab)*cos(alpha) <=> cos(alpha) = (b² - a²)/(2a² + 2ab)
Den Ausdruck rechts kann man noch kürzen:
b²-a² = (b+a)(b-a)
2a² + 2ab = 2a(a+b)
Damit ist der Ausdruck erst mal:
(b+a)(b-a)/(2a*(a+b))
a+b = b+a weswegen sich b+a und a+b weggkürzen.
Also ist der Ausdruck nur (b-a)/(2a).
Jetzt musst du auf beiden Seiten den Arcuscosinus ziehen, das ist die Umkehrfunktion der Cosinus-Funktion, und erhältst:
alpha = cos^-1((b-a)/(2a))
Natürlich ist alpha von den Längen von a und b abhängig!
Aber wenn du auf deine Skizze guckst, siehst du, dass b > a ist.
Und wie man von alpha auf beta kommt, habe ich ja bereits oben geschrieben!
Ich hoffe ich konnte dir helfen! :)
JTR

Hallo,
die Aufgabe ist ohne weitere Angaben nicht lösbar.
Mach es Dir über eine Konstruktion klar:
Du legst eine beliebig lange Seite b hin.
Nun wählst Du einen Winkel zwischen 0 und 90° (0 ausgeschlossen).
Etwa 25°.
Den legst Du in Punkt A auf der linken Seite von b an.
Auf dem freien Schenkel trägst Du die Seite a ab.
Oben ziehst u eine Parallele zu b und trägst auch hier die Seite a ab.
Nun legst Du von hier aus einen Winkel ab, der den bei a zu 180° ergänzt, also 155° in diesem Fall.
Den Schnittpunkt des freien Schenkels mit b nennst Du B.
Du hast das gewünschte Trapez, kannst es aber mit allen möglichen Winkeln zwischen 0 und 90° konstruieren.
Herzliche Grüße,
Willy

Ich kenne diese Aufgabe übrigens. Es gibt noch eine Zusatzbedingung, die Du nicht erwähnt hast:
AC=BD=b, die beiden Diagonalen sind also genauso lang wie die Grundseite b.
Dann kann man es lösen.
Trapez ABCD mit AB=AC=BD=b, BC=CD=AD=a
Dann ist das Dreieck ABC gleichschenklig mit den beiden Schenkeln b (AB und AC).
Winkel BAD und ABC=Phi
Winkel BCD und ADC=(180°-Phi), Nebenwinkel vom Stufenwinkel.
Winkel BAC ist dann 180°-2Phi.
Wegen der Symmetrie des Trapezes ist die Diagonale AC gleichzeitig die Winkelhalbierende von Phi. Somit ist
Winkel BAC nicht nur 180°-2Phi, sondern auch Phi/2.
Also: 180°-2Phi=Phi/2
Phi/2+2Phi=180°
(5/2)Phi=180°
5Phi=360°
Phi=72°
Damit haben die beiden Winkel an der Basis des Trapezes, Alpha und Beta, je 72°, die anderen, Gamma und Delta, je 108°, denn alle vier Winkel ergänzen sich zu 360° (Innenwinkelsumme eines Vierecks) und Alpha=Beta; Gamma=Delta.
Willy

Wenn Du das Ding konstruieren möchtest - drei Seiten a gleich lang, Seite b gleiche Länge wie die Diagonalen - konstruierst Du ein regelmäßiges Fünfeck und machst es zu einem Trapez, indem Du zwei nicht benachbarte Ecken miteinander verbindest.
Willy

Übrigens verhält sich dann b zu a wie 1 zu √(2-2*cos (36°))
Das ist 1 zu 0,618033989, die Zahl des Goldenen Schnitts.

Ich habe das nicht vergessen zu erwähnen.. eher derjenige der es mir gezeigt hat 😂

Die Innenwinkel sind hier arccos((b-a)/(2a)) bzw. arccos((a-b)/(2a)) groß.
Ohne genauere Angaben, lassen sich die Winkel nicht genauer bestimmen.

So wie in jedem Viereck: 360°.

Mal wieder ein komplett unnötige Antwort. Es geht darum wie ich die Innenwinkel ausrechne und nicht, dass sie insgesamt 360° ergeben

Ok, Ergänzung zu Kathinka's Law: Auch bei GF heißt eine Frage zu stellen nicht, die Antwort zu erhalten, welche man sich wünscht.
Das heißt die längere Kathete ist a^2-( (b-a)/2 )^2 ?