Injektiv oder Bijektiv?
Hallo,
auch nach langer Internet Recherche kann ich mir noch nicht genau vorstellen was ie beiden Begriffe im Betreff meinen und noch weniger wie ich das bei einer Funktion nachweisen kann. Ich habe die Funktion f(x)=3-0.5x für R für R wie belege ich was sie ist ?
Vorab vielen Dank für die Hilfe.
3 Antworten
Grundsätzlich bedeutet eine Funktion y = f(x) oder Abbildung X --> Y (X auf Y), dass jedem Element von X ist ein Element aus Y zugeordnet wird.
Jetzt: Kein Element aus Y ist mehr als ein Element aus X zugeordnet, Elemente aus Y können auch "leer" ausgehen. Kürzer:
Jedem Element aus Y ist höchsten ein Element aus X zugeordnet.

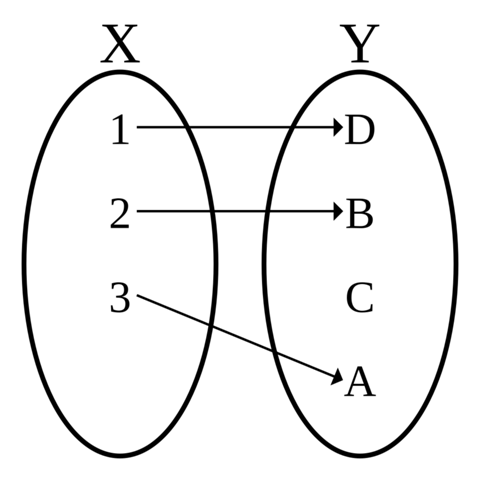
Das ist injektiv.
Dagegen könnte jedem Element aus Y auch ein oder mehrfach ein Element aus X zugeordnet werden. Kein Element aus Y ist ohne Zuordnung.

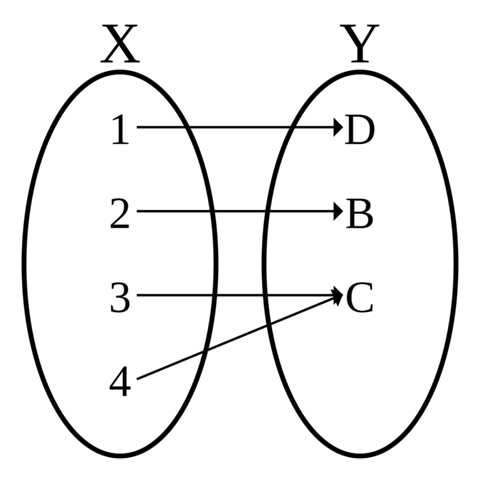
Das ist surjektiv.
Und gibt es für jedes (!) Element aus Y genau eine Zuordnung aus X:

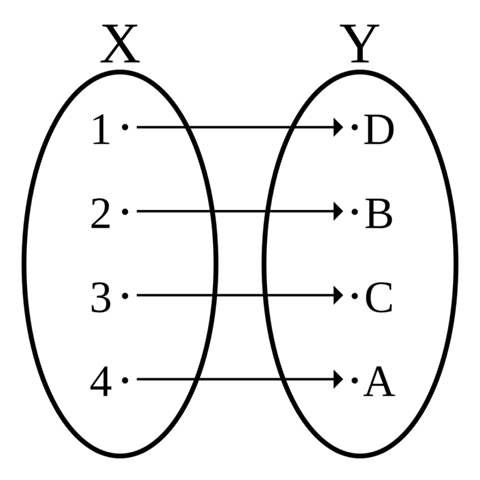
Dann ist as bijektiv.
ist eine Funktion über einen Zahlenraum injektiv? Ja, falls die Umkehrfunktion eindeutig ist.
Ist sie surjektiv? Ja, falls es kein absolutes Mini- oder Maximum gibt.
Ist sie bijektiv? Ja, falls sie injektiv und surjektiv ist.

Die anderen haben es sehr verständlich erklärt. Wenn du es beweisen willst, würde ich dir die formalen Definitionen empfehlen. Bei der injektivität kannst du das selbe aber mit ungleich statt gleich beweisen

injektiv: Jeder Wert der Wertemenge 𝕎 kommt höchstens 1 mal vor
surjektiv: Jeder Wert der Wertemenge 𝕎 kommt mindestens 1 mal vor
bijektiv: injektiv und surjektiv
Jede Gerade mit einer Steigung ungleich 0 (m ≠ 0) ist als Funktion f:ℝ → ℝ, x → f(x) bijektiv. Man kann zu jedem y ∈ 𝕎=ℝ (durch Auflösen der Gleichung y=f(x) nach x) genau ein x ∈ 𝔻 = ℝ finden.
dementsprechend ist f(x)=3-0,5x bijektiv oder ?