Hexadezimalzahlen wofür?
ich mache zurzeit eine ausarbeitung für die schule über binär und hexadezimalzahlen. ich bin soweit auch schon fertig, aber ich verstehe immer noch nicht wofür diese hexadezimalzahlen da sind! binärzahlen sind 0 und 1 und das braucht man bei computern, aber wenn man diese zahlen dann in hex umwandelt sind es doch wieder fast normale zahlen, dann kann man ja eigentlich auch gleich die richtigen nehmen ? klingt vielleicht alles ziemlich dumm, aber das referat ist leider sehr wichtig und ich muss alles genau verstehen! vielen dank schon mal!
8 Antworten
Die Hexadezimalzahlen sind einfach praktisch, weil sich eione Bit-Darstellung ohne komplizierte Rechnerei direkt hin und her umgeformt werden , man muss praktisch nur addieren zu können
Hast du eine Hexadezimalziffer, die ja die Werte von 0 bis 16 annehmen kann, dann prüfe die Zahl, ob sie größer oder gleich 8 ist, wen ja, ziehe 8 ab, und das höchstwertige Bit ist 1, sonst 0.
Jetzt frage, ob der Rest größer oder gleich 4 ist, wenn ja ziehe die 4 ab, dann ist auch das nächste Bit 1, sonst 0,
Mit dem Rest stelle die Frage mit 2, ist die Zahl . gleich oder größer 2, ist das 3. Bit 1, und der Rest ist dann ngleich das 4. Bit
Schneller und einfacher kann nan binäre Daten nicht in einer kompakten Form darstellen
Na gut, mach ichs mal Textz-Grafisch :-)
Angenommen die binäre Darstellung ist
1 0 0 1 1 1 0 1
Dann m
teils du das in 4er Gruppen
1 0 0 1 | 1 1 0 1
Die einsen multiplizierst du von rechts steigend mit
8 4 2 1 | 8 4 2 1 - entsprechend der Stellenzahl, die ja beim binären System eine Verdoppelung, szatt wie im Dezimalsystem eine Verzehnfachung darstwellt.
Daraus ergibt sich
8 0 0 1 | 8 4 0 1
Die jeweiligen 4er Gruppen addiert man, und kommt so zu
9 | 13 imd 13 ist im hexadezimalsystem C
das heißt 10011101 = # 9C - und das ist einfach, zu einer Zeit, als man Programme noch als sogenannten Hexdump abtippen musste viel leichter abzuschreinen und zu kontollieren, als eine endlose Folge von Nullen und Einsen: Tippe das mal ab, ohne dabei auch nur einen Fehler zu machen:
011101010011000101101011101011101010000101000101110111100
oder das gleiche Hexadezimal dargestellt:
0F 67 DE FA 9B 5F 22 7E
Damit du das tun kannst, was du gerade tust, nämlich mit einem Computer herumspielen. Zur optimalen Ausnutzung seiner Ressourcen bedient er sich nämlich der hexadezimalen Verschlüsselung. Frühere Computer, die es nicht taten, waren wesentlich langsamer.
Er hat sogar noch die Zeit, uns langsame Menschen zu informieren.
Hexa-Zahlen sind Gruppierungen von Binärzahlen, die eine optimale Zusammenstellung erlauben. 2^4 = 16.
Damit steht und fällt das ganze System.
"hexadezimalen Verschlüsselung" - nein. Codierung vielleicht, aber eine Verschlüsselung ist etwas anderes.
Ich neige nicht zur Rechthaberei.
Aber du guckst trotzdem mal gelegentlich nach dem Synonym für Codierung?
Hexadezimalzahlen fassen 4 Binärzahlen zusammen, das macht es kompakter
Die kleinste adressierbare Adresse und der kleinste Variablentyp ist Byte.
(natürlich gibt es auch Flags, aber die sind intern für andere Aufgaben reserviert; natürlich gibt es auch bool {oder boolean}, aber der wird intern in Byte {bei den meisten Sprachen sogar auf aktuelle Architektur, also 64 Bit} hochgerechnet! )
1 Byte sind 8 Bits, aber die ersten 8-Bit CPUs hatten nur wenige teure Segmentanzeigen: man fasste 4 Bits zusammen zu einem anzeigbaren Element (Buchstabe=char), dass von 0...9...F ansteuerbar war.
So konnte man 1 Byte = 8 Bits = 2 * 4 Bits mit 2 Segmenten 00...FF darstellen.
(bei dezimaler Anzeige hätte man 3 Segmente gebraucht und viele Bits verschenkt, denn mit 3 Segment-Anzeigen hätte man viel weiter zählen können)
Mit jeder neuen CPU-Generation wurde die Bit-Anzahl verdoppelt:
8 -> 16 -> 32 -> 64 Bit
d.h. es kommen nur neue "Segmente" (4er Bit-Gruppen) hinzu, ohne dass sich an den alten Strukturen und Bit-Positionen was ändert!
So konnte man beim Umstieg von 16 auf 32 Bit Programmen an die vorhandenen Befehle vorn ein Byte anhängen -> und daraus wurde ein 32 Bit-Befehl (so konnte man selbst mit einem 16Bit Pascal-Compiler 32-Bit Programme schreiben, ohne auf die teure Software warten zu müssen!).
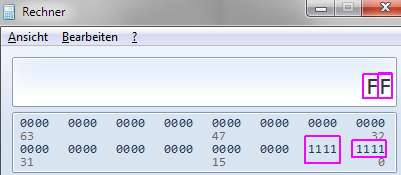
Der Windows-Taschenrechner hat eine sofortige Wandlung von Hex in Bit -> siehe Bild.
Noch was zum Vorteil von Hex: Da ich 13,3 TB dezimale Nachkommastellen von der Kreiszahl Pi habe, hat eine Komprimierung sehr großen Einfluss auf die Anzahl der nötigen Festplatten! Selbst die beste ZIP oder RAR Komprimierung (die in der höchsten Stufe richtig langsam wird!) kommt nicht an den Komprimierungsfaktor (und Geschwindigkeit!) vom ycd Format heran, dass je 19 Ziffern in ein 64Bit Hex-Wert intern ablegt! So spare ich nicht nur Festplatten, sondern komme auch noch schneller zum Ergebnis, wenn ich Ziffernfolgen suche ( mit 128Bit Befehlen und Multitasking über 80 mal schneller als normale Windows Suche: statt über 1 Woche nun weniger als 3 Tage)
Noch was zur 8, also warum man nicht 10 Bits zusammenfasste:
weil 2 hoch 3 = 8 -> so kommt es zu keiner Bit-Verschiebung, d.h. die unteren Bits bleiben bei Vergrößerung des Registers unverändert!
Oder XOR Funktion (z.B. beim Übereinanderlegen von Bildern wie Mauszeiger, damit Hintergrund unverändert bleibt
https://en.wikipedia.org/wiki/Exclusive_or
): Wenn man eine sehr große Zahl hat, kann man viele Aufgaben im Kopf berechnen:
FFFFFFFFF XOR F0 =
FFFFFFF0F
Mit Worten: tausche vom vorletzten 4er-Bit-Block alle 1 durch 0 aus
(68719476735 XOR 240 ist nicht so einfach)
siehe
http://www.wolframalpha.com/input/?i=68719476735+XOR+240
Viele Algorithmen haben was mit der 2er Potenz zu tun. So kann man einzelne Pi Nachkommastellen im Hex-Format berechnen, ohne die Billionen Stellen davor berechnen zu müssen! (
https://de.wikipedia.org/wiki/Bailey-Borwein-Plouffe-Formel
)
Eine Stelle im Hexadezimalsystem enspricht einem Nibble also 4 Bit somit sind zwei Stellen ein Byte.
Du kannst also im Hexadezimalsystem mit 0x00 bis 0xFF alle Zahlen schreiben die in einem Byte Platz haben, wenn du zwei Bytes hast dann passen da die Zahlen 0x0000 bis 0xFFFF rein usw.
vielen dank, gibt es dazu vielleicht irgendwas grafisches? ich verstehe das noch nicht 100% aber das wäre der perfekte beweis für die umrechnung!