Hängebrücke ausrechnen?!
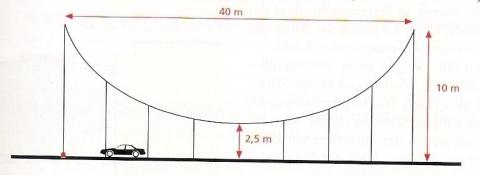
Ich sitze an der Aufgabe seit heute Nachmittag und verstehe sie einfach nicht. Ich bitte um Hilfe!Wie lautet die Gleichung der parabelförmigen Stahlkonstruktion der Hängebrücke,wenn der Ursprung in der linken unteren Ecke der Brücke (auf Straßenniveau) liegt?
4 Antworten
Die Scheitelpunktform einer Parabel ist:
y = ( x - d ) ^ 2 + e
mit
d: Verschiebung des Scheitelpunktes der Parabel gegenüber dem Ursprung nach rechts
e: Verschiebung des Scheitelpunktes der Parabel gegenüber dem Ursprung nach oben
.
Da der Ursprung der linke untere Punkt der Brückenkonstruktion sein soll, ist der Scheitelpunkt S der Parabel S ( 20 | 2,5 ). Er wurde also um
d = 20 m
nach rechts und um
e = 2,5 m
nach oben verschoben.
.
Die Parabelgleichung lautet daher, (mit noch unbekanntem Streckungsfaktor a):
y = a * ( x - 20 ) ^ 2 + 2,5
.
Der Streckungsfaktor a lässt sich nun ermitteln, indem man die Koordinaten eines beliebigen bekannten Punktes der Parabel (allerdings nicht den Scheitelpunkt!) in die berechnete Parabelgleichung einsetzt.
Ich nehme der Einfachheit halber den Punkt ( 0 | 10 ) - der Zeichnung kann entnommen werden, dass dieser Punkt auf der Parabel liegt.
Also:
10 = a * ( 0 - 20 ) ^ 2 + 2,5
<=> a * 400 = 7,5
<=> a = 7,5 / 400 = 0,01875
.
Damit lautet die Funktionsgleichung der Parabel:
y = 0,01875 ( x - 20 ) ^ 2 + 2,5
Wie kommst du auf 20???
Nun, bei jeder Parabel liegt die x-Koordinate xs des Scheitelpunktes genau in der Mitte zwischen zwei Stellen x1 und x2, an denen die Funktionsgleichung der Parabel den gleichen Wert liefert.
Da die Brücke bei x1 = 0 eine Höhe von 10 Metern hat und ebenso bei x2 = 40, ist die x-Koordinate xs des Scheitelpunktes genau die Mitte zwischen 0 und 40, also xs = 20.
.
Hast du 10 von 2,5 abgezogen und warum???
.
Ich habe nirgends 10 von 2,5 abgezogen ...
.
Bezieht sich deine Frage auf diesen Rechengang?
10 = a * ( 0 - 20 ) ^ 2 + 2,5
<=> a * 400 = 7,5
<=> a = 7,5 / 400 = 0,01875
.
Danke für's Sternchen.
ich würde die y-Achse durch die miite legen und y=ax²+2,5 und jetzt (20/10) einsetzen und a berechnen.
klar, aber dann liegt der ursprung nicht mehr in der linken unteren ecke....hier liegt er ja bei sagen wir mal S(0/2,5)
auf P(20/10) kommt man so:
der Ursprung (Scheitelpunkt) ist der punkt, an dem wir das koordinatensystem angesetzt haben.
.
somit halbierst du sozusagen die 40m in +20m und -20m.
.
die x-achse liegt auf fahrbahnhöhe, somit liegt der Scheitel jetzt auf S(0/2,5)
.
die 10m stimmen dadurch ja noch.
.
dann kannst du den punkt P(20/10) ablesen
mit der unteren Ecke.... hab ich ignoriert, weil wegen Symmetriees besser ist, die y-Achse durch die Mitte zu legen
aber wenn ich das richtig sehe, ist es doch eigentlich völlig unmöglich den ursprung in die linke untere ecke zu packen....
die aufgaben stellung macht grad ziemlich wenig sinn....das würde ja in dem fall bedeuten, dass das trageseil sinnlos unter der brücke rum baumelt
mit stahlkonstruktion könnte aber auch die fahrbahn gemeint sein....
das wär dann x^0 was aber wegen dem parabelförmig wenig sinn macht
Ich hab nur die Aufgabe abgeschrieben.Ich finde es genauso sinnlos.
y = ax^2 + 2,5
10 = 400a +2,5
a= ....
Woher weißt du das du die Zahlen so eintragen musst???Ich kenne die Formel auch,aber ich wusste nicht welche Zahlen wo hingehören.
achso.... du hast ja den punkt P(20/10) dann ist 20 der x-wert (horizontal; nach rechts positiv, nach links negativ)
10 ist dann der y-wert (vertikal; nach oben positiv, nach unten negativ)
Wie 20 und 10?!Das steht doch nicht in der Aufgabe.
Wie kommst du auf 20???