Quadratische Funktion- Funktionsgleichung finden?
Eine 6 Meter hohe Brücke hat einen parabelförmigen Bogen. Ihre Spannweite beträgt 40 Meter. Trage den Faktor a in die Funktion ein. y= ax^2
Funktionsgleichung lautet: y = _____ x²
Wie löse ich diese Aufgabe? Ich weiß, dass y= 6 ist aber wie ich da weiter mit umgehe ist mir nicht ganz klar. kann einer von euch mir helfen?
Danke schonmal :)
3 Antworten
Parabel symmetrisch zur y-Achse:
f(x) = ax² + c
Arbeitsvorstellung: ax² + c = y
Die Öffnung ist nach unten, also erst mal ein Minus.
Bei x = 0 ist y = 6.
a * 0² + c = 6 ==> c = 6
Und bei x = 20 ist y = 0.
a * 20² + 6 = 0
400 a = -6
a = -6/400
a = -3/200 oder
a = -0,015
Daher sieht die Parabel so aus:
f(x) = -0,015 x² + 6
Eine Skizze kann helfen. Ich gehe auch davon aus, dass der Bogen nach unten geöffnet ist.
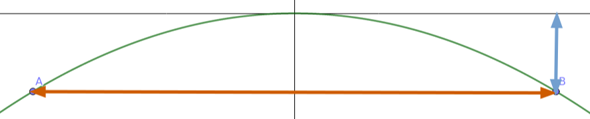
Der orangene Pfeil ist 40 m lang. Welchen x-Wert hat Punkt A oder B dann?
Die Hälfte von 40, also 20 oder -20. Und die y-Koordinate von A und B ist -6.
A(-20|-6)
B(20|-6)
Einen der Punkte setzt du in die vorgegebene Form, y = ax², ein und bestimmst a.
Bpsw. A:
y = ax²
x = 20 und y = -6
-6 = a*20²
Das sieht doch lösbar aus.
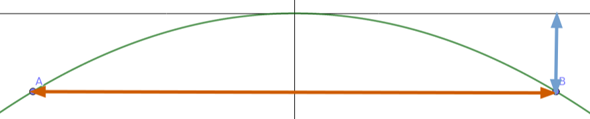
Du weißt, dass der Abstand Mittelpunkt (dem höchsten Punkt des Bruckenbogens) bis zum Rand des Brückenbogens 20 Meter ist. Auf diesen 20 metern fällt der Bruckenbogen (y-koordinate wie du richtig sagst) um 6 meter. Nornalerweise würde eine parabel auf dieser Strecke um 20^2= 400 meter fallen. Um von 400 auf 6 zu kommen musst du die 6/400 rechnen. Der Faktor a ist also 6/400=0,015
Bzw eher - 0.015 wenn wir davon ausgehen dass es sich um eine normale Bogenbrücke handelt.