Habe ich diese Mathe Übung richtig gelöst?
Das Volumen einer regelmäßigen viereckigen Pyramide mit quadratischer Grundfläche beträgt 224 Kubikzentimeter. Die Diagonale der Basis beträgt 10 cm. Finden Sie die Seitenfläche der Pyramide.

1 Antwort
50 wäre mir etwas zu großzügisch aufgerundet. Gesucht ist ja ein dreieckige Seitenfläche. Da komme ich auf 49,134 cm².
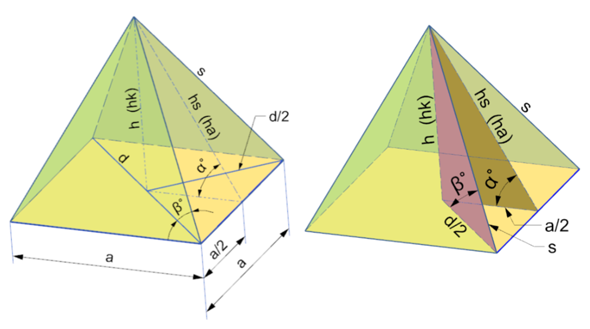
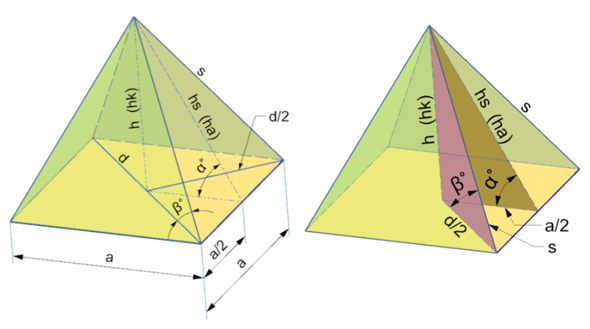
Im Prinzip muß man erst mal die Grundkante a berechnen. Dann Körperhöhe h. Aus a und h wird dann Seitenhöhe hs berechnet. Seitenhöhe hs wäre dann die Höhe des Dreiecks.
Die Fläche eines Dreiecks wird ja berechnet mit Basiskante a. Das ist ja die Kante wo ein Dreieck aufliegt. Und der Höhe h eines Dreiecks. Bei Pyramide wäre die Dreieckhöhe h die Seitenhöhe hs.
Berechnung wie folgt
---
Gesucht: Seitenfläche
Geg.: V = 224 cm³ ; d = 10 cm
---
a = Wurzel(d² / 2)
a = Wurzel(10^2 / 2)
a = 7,071067 cm
---
h = (V * 3) / a²
h = 224 * 3) / 7,071067^2
h = 13,44 cm
---
hs = Wurzel(h² + (a/2)²)
hs = Wurzel(13,44^2 + (7,071067/2)^2)
hs = 13,897251 cm
---
Seitenfläche = a * hs / 2
Seitenfläche = 7,071067 * 13,897251 / 2
Seitenfläche = 49,13419647 cm²
Ich weiß, dass die seitliche Fläche = 1/2 × Umfang der Basis × Apothem ist. Wie findet man Apotemen? Gibt es eine Formel? Da ich nicht wusste, wie ich das Apothem finden sollte, nahm ich es einfach gleich der Höhe
Na das solltest du aber wissen. Die Bezeichnungen bei einer Pyramide. Das ist die Grundkante. Die Kanten der Grundfläche nennt man Grundkante a. Schau auch mal auf folgendes PDF-Blatt. Da ist ein Bild mit den allgemein gültigen Bezeichnungen bzw. Abmessungen der Pyramide.
http://texxtorr.bplaced.net/gf/Berechnungen/Pyramide/Formeln%20fuer%20Quadratpyramide%20208.pdf
Ich versthe e es nicht. Kannst du bitte noch einmal erzählen?