Gibt es eine funktion 2.grades die eine gerade ist?
Es gilt ja: der grad einer Funktion gibt die maximalste Anzahl an existierenden nullstellen wieder. Somit könnte es auch nur eine nullstelle haben (gerade)
?
6 Antworten
Hallo,
eine Funktion zweiten Grades mit einer Nullstelle ist eine Parabel, deren Scheitelpunkt auf der x-Achse liegt. Das macht sie aber nicht zu einer Geraden.
Die Ableitung einer Parabel ist eine Gerade, die immer noch von einer Variablen abhängig ist. Deswegen kann eine Funktion zweiten Grades keine konstante Steigung wie eine Gerade besitzen.
Herzliche Grüße,
Willy
Eine Funktion 2. Grades ist nie eine Gerade, kann aber nur eine (eigentlich zwei gleiche) Nullstellen haben.
Die rot gezeichnete Funktion 2. Grades hat nur eine Nullstelle. Eine Gerade ist es aber deswegen nicht.
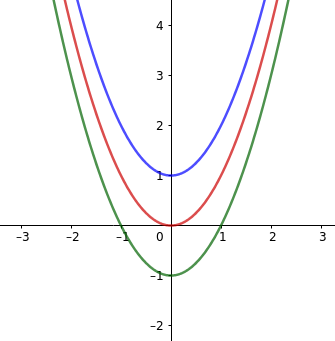
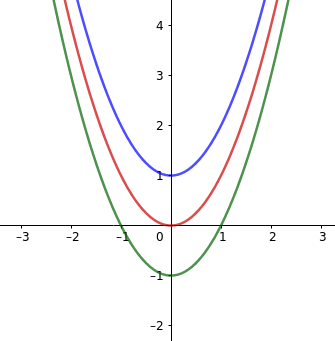
Nehmen wir mal eine Funktion zweiten Grades an: f(x)=ax²+bx+c. Damit das eine Gerade ist, muss es eine Konstante Steigung haben. f'(x) darf nicht mehr von x abhängen. f'(x)=2ax+b. Das ist nur der Fall, wenn wir für a Null einsetzen, aber dann ist es keine Funktion zweiten Grades mehr, also ist das unmöglich.
Fehlschluss: Nur eine Nullstelle zu haben bedeutet nicht, dass die Funktion eine Gerade ist, nur weil eine Gerade auch nur (maximal) eine Nullstelle hat.
Die Funktion f(x) = x^2 hat auch nur eine Nullstelle, ist aber keine Gerade.
... die beide Null sind.
Schau mal "algebraische Vielfachheit" und "geometrische Vielfachheit" an.
PS: "Maximalst" gibt's nicht. "Maximal" kann nicht gesteigert werden.
X^2 hat eine doppelte nullstelle