Wieso kann eine Funktion 3. Grades nur höchstens 3 und mindestens 1 Nullstelle haben?

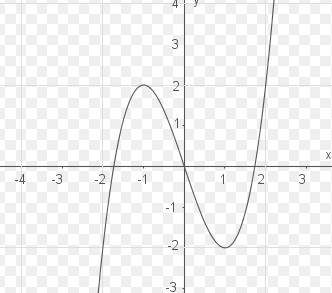
Schau dir den Graphen an, verschiebe ihn entlang der Y-Achse soviel du willst es wird immer mindestens eine Nullstelle haben. Bei manchen Punkten aber auch mal drei.

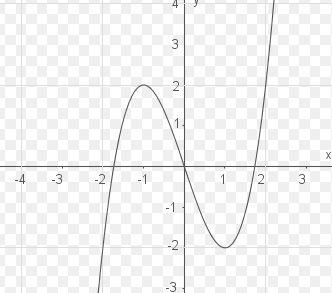
Gäbe es eine Polynomfunktion 3. Grades mit mindestens 4 Nullstellen so hätte deren Ableitung nach dem Satz von Rolle mindestens 3 Nullstellen, die zweite Ableitung mindestens 2 Nullstellen und die dritte Ableitung mindestens eine Nullstelle. Das kann aber nicht sein, da die dritte Ableitung konstant und ungleich 0 ist.

Um zu zeigen, dass es mindestens eine Nullstelle gibt, musst du dank dem Zwischenwertsatz nur zeigen, dass es für jedes normierte Polynom p(x)=x^3+a2*x^2+a1*x+a0 Werte x1,x2 gibt, so dass p(x1)<0 und p(x2)>0 gibt. Zum Beispiel x1=-3M und x2=3M mit M=max(1,|a0|,|a1|,|a2|) funktioniert.