Ganzrationale Funktion Kurven?
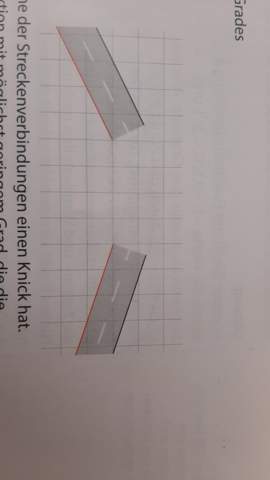
In der Abbildung sieht man zwei Straßenstücke. Diese sollen durch ein Kurvenstück verbunden werden.
Aufgabenstellung: Wählen Sie ein geeignetes Koordinatensystem und bestimmen Sie eine quadratische Funktion, deren Graph die beiden roten Fahrbahnränder verbindet. Zeigen Sie, dass mindestens eine der Streckenverbindungen einen Knick hat.
Die roten Ränder sind halt der untere Teil der Straße.
Ich check die Aufgabe nicht... danke im vorraus :)
2 Antworten
Wählen Sie ein geeignetes Koordinatensystem
Geeignet ist ein Koordinatensystem dann, wenn es möglichst bequem zur Lösung führt. Faulheit und Bequemlichkeit sind in der Mathematik Tugenden.
Dazu lege ich die x-Achse durch die Endpunkte der roten Linien, die y-Achse genau in die Mitte davon und als Skala wähle ich 1 Kästchen = 1
Dadurch habe ich schon mal 2 Nullstellen für die quadratische Funktion und wähle deshalb die Nullstellenform:
f(x) = a * (x - 2) * (x + 2)
Das überführe ich mit der 3. binomischen Formel in die Normalform:
f(x) = a * (x^2 - 4) = ax^2 - 4a
Nun müssen wir noch a bestimmen und brauchen dazu eine zusätzliche Information. Diese entnehmen wir der Skizze und stellen fest, dass bei der Nullstelle x = 2 die Steigung des ankommenden Straßenstückes = -1/3 beträgt. Damit es keinen Knick gibt, sollte auch die Funktion an dieser Stelle die Steigung -1/3 haben.
Also leiten wir erstmal ab:
f'(x) = 2ax
Und setzen ein:
-1/3 = 4a
a = -1/12
Damit lautet die Funktion:
f(x) = -1/12 x^2 + 1/3
So sieht der Straßenverlauf dann aus:
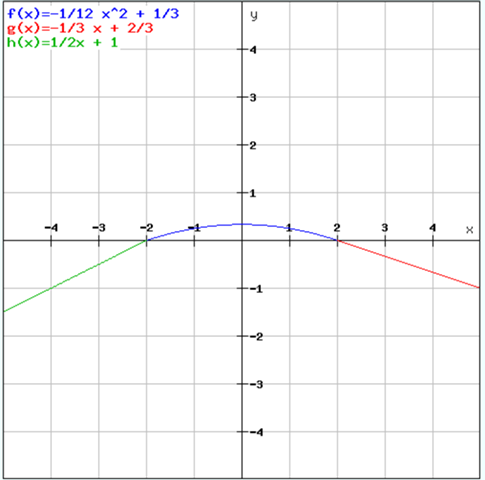
b)
Nun berechnen wir die Steigung von f(x) an der Stelle x = -2:
f'(x) = 2ax
mit a = -1/12 ergibt sich:
f'(x) = -1/6 x
x = -2 eingesetzt:
f'(-2) = 1/3
Aus der Zeichnung lesen wir aber ab, dass das von links ankommende Straßenstück eine Steigung von 1/2 hat. Hier gibt es also den Knick.
Da wir die y-Achse in die Mitte gelegt haben, ergibt sich eine zur y-Achse symetrische Parabel.Damit gilt:
f(x) = -f(-x)
und:
f'(x) = -f'(-x)
Daraus folgt:
⎮f'(x)⎮= ⎮f'(-x)⎮
Das ist aber bei den ankommenden Straßen nicht der Fall, also muss es einen Knick geben.
Weil f' immer die Steigung der Kurve angibt. Und da die gleich sein muss, wie die des geraden Stücks, und das hat 1/3, kann man f' = 1/3 setzen, damit es keinen Knick gibt.
Na dann lege doch die x-Achse genau durch die Endpunkte der beiden roten Linien und die y-Achse genau in die Mitte zwischen den beiden Linien. Dann kannst du durch die beiden Punkte (-1|0) und (1|0) eine quadratische Funktion legen (verwende die Darstellung in Nullstellenform) und mußt dir nur noch über den Streckungsfaktor Gedanken machen.
Dankeschön:) Warum kann ich bei der Ableitung die Steigung einfach für f'(x) einsetzen?