Funktion anhand Extremstellen berechnen?
Eine Funktion g(x) besitzt an den stellen x1=-2 und x2=0 Extremstellen. Ermitteln Sie rechnerisch eine Mögliche Funktionsgleichung der Funktion g(x).
Kann mir da bitte jemand helfen? Wir sollen das für Mathe machen, aber haben sowas noch nie gemacht.
Welche Klasse ? Gym ?
Ich bin in der 11 Klasse auf einem Gymnasium
2 Antworten
2 Extremstellen kann es erst ab Fkt dritten Grades geben .
.
Mit diesen Angaben ergeben sich unendliche viele Fkt.
.
Man muss von der Ableitung ausgehen
f'(x) = a*(x+2)(x+0) , denn diese hat bei x = - 2 und x = 0 Nullstellen ,was Extremstellen in f(x) bedeutet
f'(x) = ax² + 2ax
.
Jetzt integrieren
F(x) = 1/3*a*x³ + 1/2 * 2 * a * x =
a/3 * x³ + ax²
.
Irgendeine Zahl für a nehmen
.
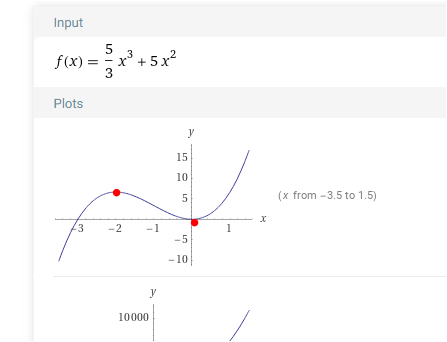
f(x) = 5/3 * x³ + 5x²
.
Graph
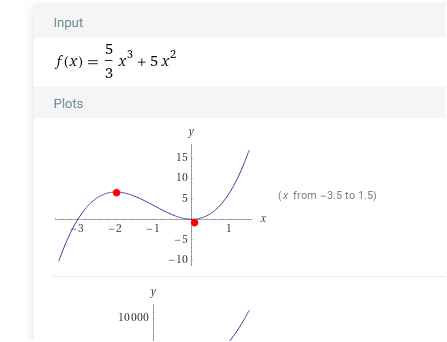
passt . Mit a = -5 würde aus dem HP ein TP , aus dem TP ein HP werden
.
Ok , wenn man noch nicht integrieren kann , dann dieser Weg :
Fkt DrittenGrades
f(x) = ax³ + bx² + cx + d................d kann man erstmal als Null annehmen (s.u)
f'(x) = 3a² + 2bx + c
.
Damit bei x = 0 ein Extremum ist , muss gelten
0 = 3a*0² + 2b*0 + c
Das geht nur ,wenn c = 0
.
also hat man als Ausgangspunkt f(x) = ax³ + bx²
und nutzt f'(x) = 3a² + 2bx
setzt x = -2 ein und erhält
0 = 12a - 4b
4b = 12a
b = 3a
.
.
Man kann/muss wählen , zB a = -7 , dann b = -21
.
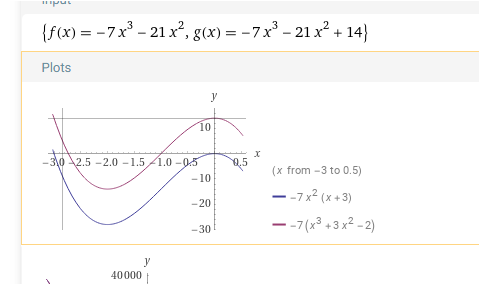
f(x) = -7x³ - 21x²
.
Man kann sogar noch eine Zahl dranhängen ,die Extrema bleiben gleich , die Fkt wird nur hochrunter geschoben . Deswegen kann man auch d als Null annehmen erst mal , damit man überhaupt zu Werten für a und b kommt.
.
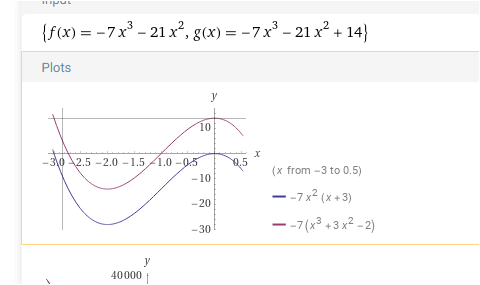
passt wieder
Wenn Du noch keine Differentialrechnung kannst, dann helfen Dir vielleicht die trigonometrischen Funktionen; cos besitzt bei x=0 ein Maximum, bei x=-2*pi ebenfalls; damit ist eine gewünschte Funktion:
g(x) = cos(pi*x)