Extremwertaufgabe mit Querschnittsfläche?

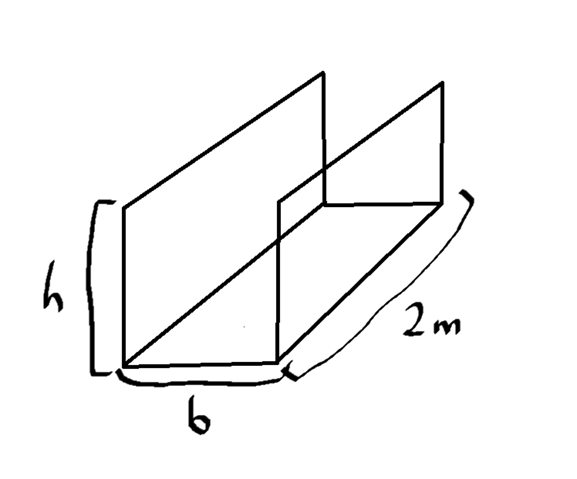
Hi habe ein Problem es geht um Extremwertaufgaben. Die Situation ist wie auf dem Bild. Die Querschnittsfläche ist 250cm² und gesucht sind h und b der Materialverbrauch soll aber minimal sein. Hat einer eine Idee? Bin für Hilfe jeder Art dankbar.

Answer 1

[fjf100]

Bei Extremwertaufgaben liefert immer die gesuchte Größe die Hauptgleichung (Hauptbedingung).

Die Hauptgleichung hat mindestens 2 Unbekannte und davon muß dann mindestens 1 Unbekannte durch eine Nebengleichung (Nebenbedingung) ersetzt werden.

Das ergibt dann 1 Gleichung der Form y=f(x)=.... wo dann die Extrema ermittelt werden,Kurvendiskussion

1) U=b+2*h ist der Umfang des U,soll minimal werden, Hauptgleichung

2) A=b*h → h=A/b in 1)

U(b)=b+2*A/b

U(b)=2*A/b+b hat die Form y=f(x)=... nun Extrema bestimmen

abgeleitet

U´(b)=0=-2*A/b²+1

spezielle Quotientenregel (1/v)´=-1*v´/v²

(1/b)´ → b´=1*b^(1-1)=1*b⁰=1 und b²=b²

0=-2*A/b²+1 → 2*A/b²=1 → b²=2*A/1

b1,2=+/-Wurzel(2*250 cm²)=+/-22,36067..cm

b=22,36 cm negativer Wert fällt weg,weil es keinen Sinn macht (negative Strecke)

nun prüfen,ob Maximum oder Minimum

U´(b)=-2*A/b²+1 abgeleitet

(1/b²) → v=b² → v´=2*b und v²=(b²)²=b⁴

U´´(b)=-2*A*(-1)*2*b/b⁴=2*A*b/b⁴

U´´(b)=2*A/b³>0 also ein Minimum

b=22,36 cm und h=A/b=250 cm²/22,36 cm=11,18 cm

Probe: A=b*h=22,36 cm*11,18 cm=250 cm

Prüfe auf rechen- und Tippfehler.

Woher ich das weiß: Studium / Ausbildung – hab Maschinenbau an einer Fachhochschule studiert

Comments

[fritzel397]

Woher kommt eigentlich bei Punkt 2) das A her was ist das?

[fjf100]

@fritzel397

Den Buchstaben A verwendet man im Normalfall für eine Fläche.

A=250 cm²=b*h

Answer 2

[tunik123]

Nimm doch eine zweite Rinne und stülpe sie kopfrum über die erste. Dann ist die Höhe 2 * h und die Fläche 500 cm². Der Materialverbrauch ist dann minimal, wenn der Querschnitt quadratisch ist, also 2 * h = b.

Answer 3

[Kaen011]

Ist das ein U Zylinder oder ist das vollmaterial? Ich versteh deine zeichnung und die aufgabt nicht richtig

Answer 4

[DerEinsiedler]

Drücke h durch b aus mit dem Wissen, dass h * b = 250 cm² ist.

Und dann minimiere die Umfangsfunktion 2 h + 2 b

Herauskommen wird h = b, weil das Quadrat immer die rechteckige Form mit kleinstem Umfang bei gleicher Fläche ist.

Comments

[tunik123]

Der Umfang ist hier aber 2 h + b.

Answer 5

[RIDDICC]

1. du musst also h·b=250cm² einhalten?
2. und dann sollst du O=2m·(b+2·h) minimieren?
3. also: h=250cm²/b=2,5dm²/b=0,025m²/b
4. und: O(b)=2m·(b+2·0,025m²/b)
5. dann O'(b) bilden...
6. Extremwert bla bla...
7. gähn
8. verstanden?

Woher ich das weiß: Studium / Ausbildung