Extremwertaufgabe?

Hallo,
Ich habe eine Frage zu der Aufgabe 10): ich verstehe nicht so ganz den Ansatz: auf jeden Fall ist die Höhe konstant und ich brauche eine Formel für den Querschnitt und habe den Umfang gegeben, nur verstehe ich nicht: wied jetzt ein quadratischer streifen genommen und in die Gestalt des sechsecks gebracht oder wie genau stellt man die Beziehung zum Umfang auf.
2 Antworten
Der Pappstreifen ist 10 cm breit und das ist dann auch die Höhe der Schachtel.
Die Länge von 50 cm des Pappstreifens ist der Umfang des (nicht gleichmäßigen) Sechsecks, also der Umfang der Grundfläche der Schachtel.
Das Volumen der Schachtel ist also Grundfläche multipliziert mit den 10 cm: V= G*10

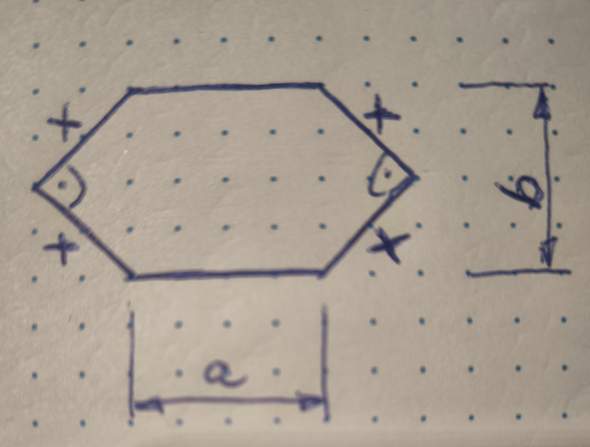
Und die Grundfläche setzt sich eben aus einem Rechteck und zwei gleichschenklig rechtwinkligen Dreiecken zusammen. Wenn du die Katheten der Dreiecke mit x bezeichnet und die Seiten des Rechtecks mit a und b setzt sich doch der Umfang wie folgt zusammen:
4*x + 2*a = 50 nach a umgestellt erhältst du dann a= 25 - 2*x (ich lasse die cm weg).
Für b ergibt sich unter Verwendung von Pythagoras b= W(2) * x wobei das W() für die Quadratwurzel steht.
Nun für die Grundfläche die Funktion aufstellen und mit den Ableitungen dann für x den Wert finden, der die Grundfläche und somit das Volumen maximal werden lässt.
Der genaue Wert von x= (1/14)*(100+25*W(2)) oder gerundet x= 9,668
In der Aufgabenstellung steht doch, dass aus einem Pappstreifen von 50 cm Länge diese Schachtel gemacht werden soll. Du hast damit die Vorgabe, dass der Umfang genau diese 50 cm sind. Und die Breite des Pappstreifens eben die Höhe der Schachtel.
Aber bezieht sich die Länge auf die Seiite oder auf den kompletten Umfang (ich dachte nämlich eine Länge a)
Auf den kompletten Umfang. Wenn du auf das Bild der Schachtel schaust, sollte das auch klar sein.
U=2*a+4*b
A=a*l+l*h
mit a als eine Seitenlänge des Rechtecks, b als Länge eines Dreiecksschenkels, h als Höhe eines Dreiecks und l als Länge der Grundseite.
damit und über entsprechende Winkelbeziehungen zwischen l, b und h sollte das eigentlich lösbar sein.
Mvg
Welchen Wert nimmst du jetzt für den Umfang ? Und wie genau kommst du auf l?
Der Umfang sind 50 cm, und auf l sollte man über sin/cos Beziehungen kommen. Ich hab es nicht ganz zu ende gedacht aber theoretisch sollte das passen. Andere Informationen/Bedingungen existieren ja nicht.
Aber wieso 50, es wird doch noch von einer Breite gesprochen?
die 50 Länge werden um die Schachtel herumgeführt und damit zum Umfang
Vielen Dank, ich verstehe alles, nur nicht, wieso der Gesamtumfang 50 ist (und nicht beispielsweise 100. Ein Rechteck hat ja 2a und 2b, wenn 2b die Höhe sind, dann müssen 2a der Umfang sein, oder wie versteht man das?