Exponentialfunktion ausklammern?
Hi ich sitze seit 2 Stunden an einer Mathe Aufgaben und ich weiß immer noch nicht wie ich sie ausklammern soll. Ich hoffe ihr könnt mir helfen und bitte auch sagen wie ihr ausgeklammert habt. Mfg
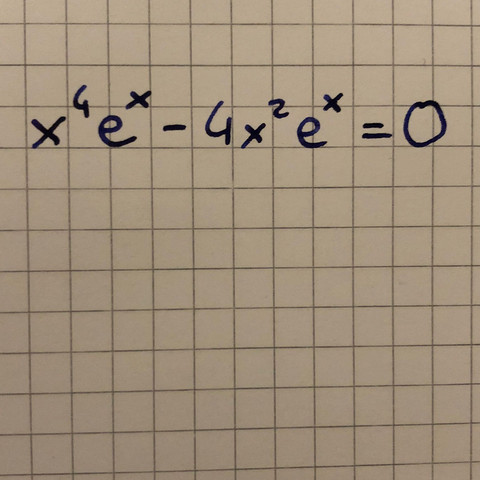
6 Antworten
x ^ 4 * e ^ x - 4 * x ^ 2 * e ^ x = 0
(e ^ x) * (x ^ 4 - 4 * x ^ 2) = 0 | : e ^ x
x ^ 4 - 4 * x ^ 2 = 0
z := x ^ 2
z ^ 2 - 4 * z = 0
z * (z - 4) = 0
Wegen dem Satz vom Nullprodukt ist z_1 = 0
z - 4 = 0
z = 4
z_2 = 4
Weil z : = x ^ 2 deshalb ist x = ∓ √(z)
x_1 = - √(z_1) = -√(0) = 0
x_2 = + √(z_1) = + √(0) = 0
x_3 = - √(z_2) = - √(4) = -2
x_4 = + √(z_2) = + √(4) = +2
Das sind die Nullstellen, die 0 ist eine sogenannte doppelte Nullstelle.
man könnte ja auch auf die idee kommen , durch e^x und x^2 zu teilen.
dann fehlten zwei NSt. Warum ist das nicht statthaft ? oder kann man automatisch sagen, wenn ich durch x^k teilen kann , habe ich sofort die NSt x= 0 und bei k = 2 doppelte, k= 3 dreifache usw .
Satz vom Nullprodukt c=a*b hier ist c=0 wenn a=0 oder b=0 oder a=b=0
also x1=0
Die Zweite Nullstelle liegt bei x2=-2 hab ich mit meinen Graphikrechner (GTR,Casio) ermittelt.
Mit normalen Mitteln kann man x2=-2 nicht ermitteln,weil x einmal im Exponenten vorkommt und einmal nicht.
Nach x auflösen geht hier nicht
Du muß eine Wertetabelle aufstellen und dann auf Vorzeichenwechsel achten.
Findet ei Vorzeichenwechsel statt,so liegt zwischen den beiden x-Werten eine Nullstelle
Hinweis: Berührt der Graph nur die x-Achse,so findet kein Vorzeichenwechsel statt.
Du mußt dann darauf achten,ob sich der Funktionswert y=f(x) sich der x-Achse nähert oder entfernt.
Man wählt x-Werte zwischen x=-4,-3,-2....1,2,3,4
Durch probieren hättest du dann x2=-2 ermittelt.
bei krummen Werten wendet man die Näherungsformeln von "Newton" (Tangentenverfahren) oder "Regula falsi (Sehnenverfahren) an.
Diese werden so oft angewendet,bis die Genauigkeit für die Nullstelle ausreicht.
Am einfachsten ist es aber mit den GTR.
Ohne solch ein Ding ,ist man aufgeschmissen.
x^2 * e^x * (x^2 - 4) = 0
schau was in beiden termen gleich ist! gehe schrittweise vor, du siehst dass e^x in beiden termen vorkommt, das kannst du rausziehen. jetzt kannst du aus dem einem term maximal noch x^2 rausziehen, und der andere term x^4:x^2 ist x^2
x^2*e^x(x^2-4)= 0
ich hab sowas schon mal gemacht :D, Übung.
Schau dir einfach an welche Basis und welche Exponenten es gibt und durch welche "Zahl" man diese teilen kann.
x^2 e^x (x^2 - 4)
Danke