Eine zum nullpunkt symetrische polynomfunktion 5ten grades hat in punkt P (0/0) die Steigung m=2 und in punkt Q(-1/0) einen Wendepunkt?
Ich muss das rechen bin aber überfordert wir geht das
2 Antworten
Wenn es heisst, dass es eine Polynomfunktion 5ten Grades ist, dann sieht die Ausformulierung so aus:
y = a*x^5 + b*x^4 + c*x^3 + d*x^2 + e*x + f
Aus des spärlichen Angaben sollst Du also 6 unbekannte Koeffizienten bestimmen. Aber ganz so heiss gegessen wird das nicht. Denn die Angabe "symmetrische Polynomfunktion" sagt, dass alle Koeffizienten mit geraden Exponenten wegfallen. Somit verbleiben nur noch drei: a, c und e. Damit wird die Sache schon etwas gemütlicher. Du musst aus den Angaben somit nur noch drei Bedingungen herauslesen.
1. Die Steigung im Punkt (0,0)
2. Der Punkt (-1 / 0) ist ein Wendepunkt was bedeutet, dass die 2. Ableitung an der Stelle -1 verschwindet.
3. der Punkt (-1 / 0) ist auch ein gültiger Punkt auf der Kurve.
Zur Veranschaulichung kannst Du Dir auch die zugehörige Grafik anschauen.
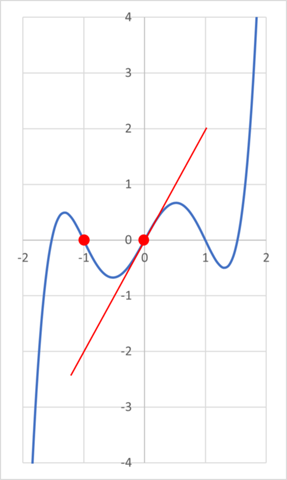
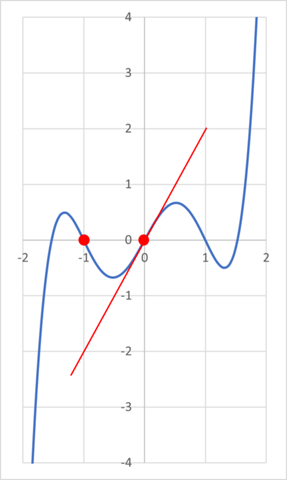
Symmetrisch zum Nullpunkt ------> nur ungerade Exponenten, also
f(x) = ax^5 + bx^3 + cx
somit nur noch 3 Unbekannte a, b, c
um diese zu berechnen stelle 3 Gleichungen auf:
1) f(-1) = 0 ................................ Punkt (-1|0)
2) f ' (0) = 2 ...............................Steigung = 2 bei x=0
3) f ' ' (-1) = 0 .......................... Wendepunkt bei x=-1
und löse das Gleichungsystem
Verständlich?