Dreieck Flächeninhalt mit Integralrechnung?
Hallo,
ich schreibe nächste Woche eine Matheklausur und ein anderer Kurs aus meiner Stufe hat folgende Übungsaufgabe bekommen:
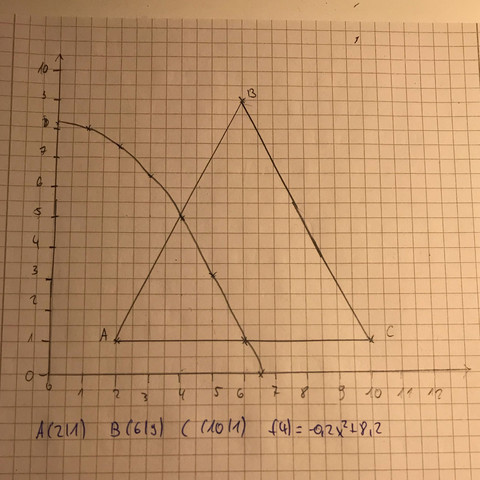
Gegeben ist das Dreieck mit den Punkten A B und C und die Funktion f(x). Die Funktion „trennt“ das Dreieck in zwei Teile, und man soll nun beide Teile einzeln voneinander mit Integralrechnung berechnen (siehe Bild).
Ich verstehe nur nicht wie das gehen soll. Den linken Teil könnte man ja eventuell mit dem Integral machen, doch dann müsste man noch was abziehen um auf den Flächeninhalt zu gelangen. Ich komme einfach nicht weiter. Es wäre toll, wenn jemand mir die Aufgabe erklären könnte.
6 Antworten
Für das linke Dreieck kann ich mir vorstellen, die 2 Seiten als lineare Funktion beschreiben und einzeln von 6 bis 2 zu integrieren bis zur quadratischen Funktion. Das 2. natürlich vom 1. Integral abziehen. Sorry, das 2. Integral von 4 bis 2!
Du verschiebst das ganze erst, dass die Strecke AC auf der x-Achse liegt.
Dann berechnest du das integral unter der Funktion zwischen 4 und 6.
Um den FlächenInhalt des linken Dreicecks zu erhalten summierst du dazu nach den, mithilfe der normalen Dreiecksformel, den Flächeninhalt des Dreiecks zwischen 2 und 4.
Den Flächeninhalt des rechten Teiles erhälst du dann, indem du den Flächeninhalt des linken von dem des großen Dreieckes abziehst.
naja, musst du halt in mehrere Abschnitte das Integral berechnen.
für das kleinere Dreiecke eben integral von A bis oberer Schnittpunkt plus integral oberer schnittpunkt bis unterer schnittpunkt.
immer die integraldifferenz zwischen den jeweiligen 2 Kurven berechnen.
ähnliches machst du beim großen.
Aber natürlich solltest du dir erst mal die 3 funktionenen für die 3 dreiecksseiten hinschreiben! :-)
mit A und B kannst du die Gerade AB (y=mx+b) aufstellen;
dann mit f den Schnittpunkt S berechnen;
dann f integrieren von S bis Schnittpunkt von AC mit f
dann kleines Rechteck unten, was zu viel ist abziehen
dann linkes kleines Dreieck mit g•h/2 berechnen
usw
Für den linken Teil berechnest du das Integral
von f(x) von 4 bis 6 und ziehst 2 ab. Dazu kommt
(4*2) /2 = 4 für den Rest der Dreiecksfläche.
Der rechte Teil ist 8*4 = 32 (die Dreiecksfläche)
minus der linke Teil.